Введение. Для современных исследований процессов, происходящих в различных сферах человеческой жизнедеятельности использование чисто эмпирического подхода оценки взаимного влияния сигналов с квадратурной амплитудной модуляцией (КАМ) [1] проблематично в связи со сложностью и параметрической емкостью используемых модулированных сигналов в телекоммуникационных системах, нелинейностью АЧХ каналов связи [2].
Комплексные показатели качества сигналов информационного обмена не предусматривает оценку их взаимного влияния в линиях связи каналов передачи данных [3].
В известных математических моделях в качестве комплексных показателей использовались коэффициенты взаимного различия, фигуры Лиссажу [3,4]. Однако в данных моделях невозможно выявить искажения сигналов, обусловленных взаимным влиянием сигналов по соседним каналам в многоканальной телекоммуникационной системе с частотным разделением каналов.
Цель исследования. Разработать математическую модель зависимости изменения радиуса сферы, как комплексного показателя взаимного влияния сигналов телекоммуникационных систем от изменения параметров сигналов с квадратурной модуляцией (КАМ) в частотно-фазовом многомерном метрическом пространстве.
Материал и методы исследования Для наглядного представления меры «близости» между процессами, ввиду многопараметрической оценки качества функционирования систем при трехмерном наглядном графическом представлении необходимо переходить в область многомерных метрических пространств. То есть, адаптировать различные координаты (декартовы, полярные) в виртуальные координаты исследуемых многомерных параметрических пространств [5,6,7]. Как следствие, можно определять влияние друг на друга сигналов различных информационных систем для выработки комплекса мероприятий по повышению достоверности информационного обмена в ТКС.
Для проведения исследования взаимного влияния сигналов (ВВС) в телекоммуникационных системах (ТКС), предлагается использовать как геометрические объемные фигуры, так и их геометрическое взаимодействие в многомерных метрических пространствах [6]. Близость сфер, размеры и положение которых в виртуальном пространстве определяется параметрами модулированных сигналов, можно использовать как комплексный показатель оценки взаимного влияния сигналов друг на друга [5,6,7].
Результаты исследования и их обсуждение На рисунке 1 представлена графическая модель определения расстояния между точками сфер, определяемыми параметрами сигналов в декартовых системах координат [6].
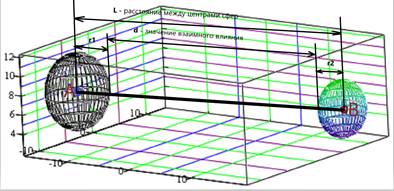
Рисунок 1 - Графическая модель определения расстояния между точками сфер, определяемыми параметрами сигналов в декартовых системах координат
Для обеспечения достоверности результатов необходимо проводить анализ строго в определенном секторе полученных сфер, адаптировать углы классических полярных координат [8] и перейти в частотно-фазовое многомерное метрическое пространство (рисунок 2а). При этом ось x заменена на ось частот ω, а ось y заменена на ось фазы φ.
Тогда коэффициент взаимного влияния сигналов можно выразить как: K=1/d, где
d=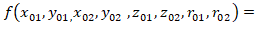
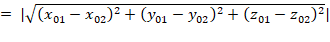
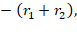 где:
где:
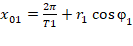 ;
; 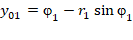 ;
; 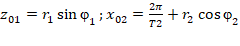 ;
; 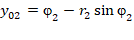 ;
; 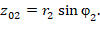
Где: r1, r2 - соответственно амплитуды первого и второго сигналов;
φ1, φ2 - соответственно фазы первого и второго сигналов;
Циклическая частота ω представляет собой выражение ω=2π/Т, где Т – период высокочастотного сигнала.
В линиях связи каналов передачи данных телекоммуникационных систем возникают мультипликативные помехи, обусловленные многолучевостью радиоканалов, затуханием сигнала в проводных линиях связи, неидеальностью входных селективных фильтров. [9,10]. В этом случае будет наблюдаться изменение радиуса сферы. На рисунке 2б представлена геометрическая модель изменения радиуса сферы, как параметрического изображения сигнала А и, следовательно, изменения расстояния между точками А и С, определяющее взаимное влияние сигналов в ТКС.
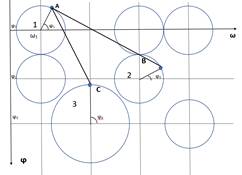
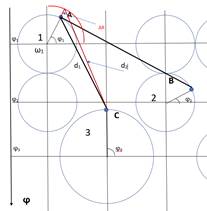
а) б)
Рисунок 2 - Графическая модель определения расстояния между сферами
Для получения выражения зависимости радиуса сферы в декартовой системе координат, как образа сигнала в многомерном метрическом пространстве от отклонений параметров модулированного сигнала необходимо рассмотреть сдвиг фазы исследуемого сигнала A и рассмотреть изменение амплитуды, частоты и фазы сигнала B.
Обозначим 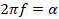 ,
, 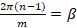 .
.
Возьмем сигнал А1 и сигнал А2, сдвинутый по фазе 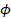 относительно А1
относительно А1
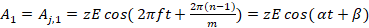 (1)
(1)
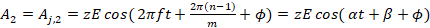 (2)
(2)
Для математического описания воспользуемся выражением окружности:
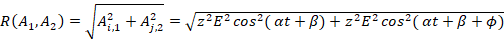 (3)
(3)
Из выражения (3) получим:
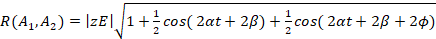 =
=
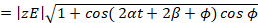 (4)
(4)
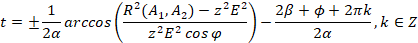
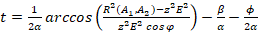 (5)
(5)
Возьмем второй сигнал В, с изменениями амплитуд несущей и амплитуд кодовых составляющих и изменения фазы:
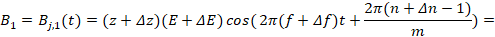
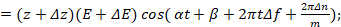 (6)
(6)
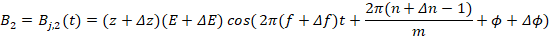
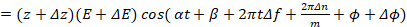 (7)
(7)
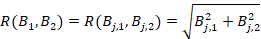
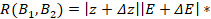
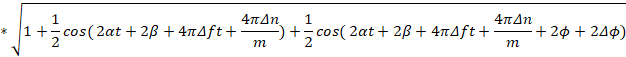
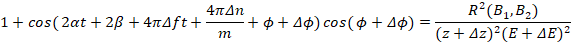
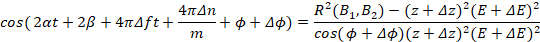
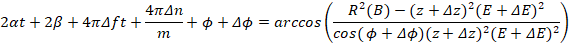
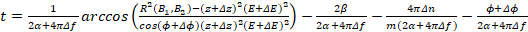 (8)
(8)
Приравнивая правые части (5) и (8) получим:
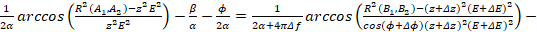
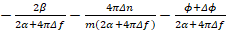 ; (9)
; (9)
Проведем математическое преобразование правых частей выражения 9:
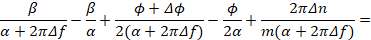
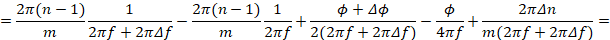
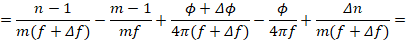
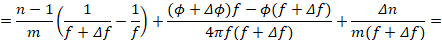
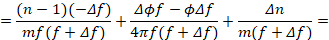
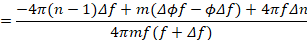
Полученный результат подставляя в (9) получим:
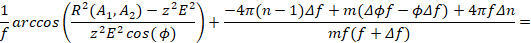
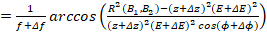 (10)
(10)
Определим условие:
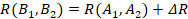 (11)
(11)
Подставляя (10) в (11) получим:
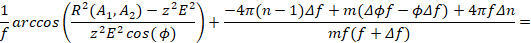
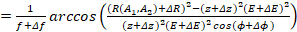 (12)
(12)
Рассмотрим функцию:
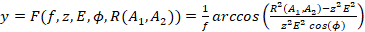 (13)
(13)
Полное приращение (12) (2.30):
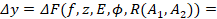
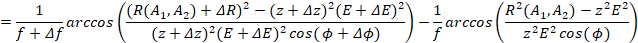
Получим:
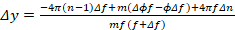 (14)
(14)
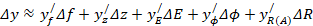 (15)
(15)
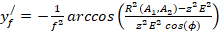 (16)
(16)
 (17)
(17)
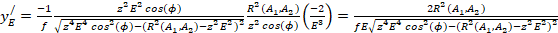 (18)
(18)
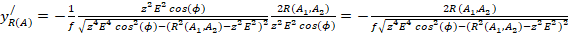 (19)
(19)
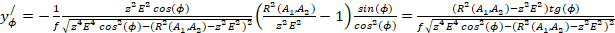 (20)
(20)
Подставляя (14,16-20) в (15), получим:
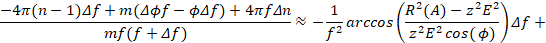
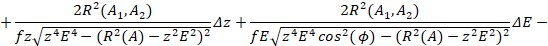
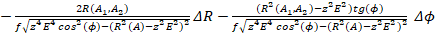 (21)
(21)
Отсюда:
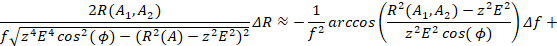
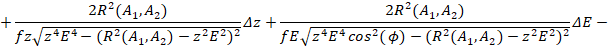
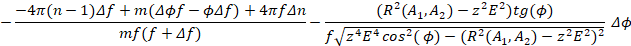
Следовательно:
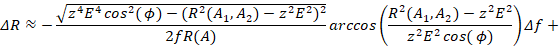
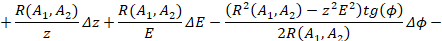
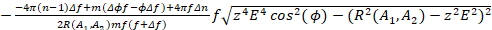 (22)
(22)
Выводы Таким образом, получена математическая модель в виде математического выражения (22), определяющее зависимость области изменения радиуса сферы от изменений частоты 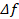 , амплитуды несущей частоты
, амплитуды несущей частоты 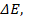 фазы
фазы 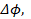 амплитуд кодовых составляющих
амплитуд кодовых составляющих 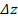 сигналов, использующих КАМ в многомерном метрическом пространстве, обусловленных взаимным влиянием сигналов в линиях связи каналов передачи данных телекоммуникационных систем. Полученная модель является комплексным показателем взаимного влияния сигналов. Использование полученной модели позволит проводить анализ зависимости изменения взаимного влияния сигналов по соседним каналам многоканальной ТКС от изменения параметров сигналов, не применяя эмпирические методы параметрической оценки, что позволит сократить временные и аппаратурные затраты и повысить достоверность информационного обмена в ТКС.
сигналов, использующих КАМ в многомерном метрическом пространстве, обусловленных взаимным влиянием сигналов в линиях связи каналов передачи данных телекоммуникационных систем. Полученная модель является комплексным показателем взаимного влияния сигналов. Использование полученной модели позволит проводить анализ зависимости изменения взаимного влияния сигналов по соседним каналам многоканальной ТКС от изменения параметров сигналов, не применяя эмпирические методы параметрической оценки, что позволит сократить временные и аппаратурные затраты и повысить достоверность информационного обмена в ТКС.
 science-review.ru
science-review.ru