Интерференция волн является одним из основных физических эффектов, широко распространенных в природе и получивших наибольшее применение в технике. Это явление заключается в перераспределении энергии поля в пространстве при наложении двух или большего числа когерентных волн любой природы. Электромагнитное излучение является одним из наиболее распространенных явлений природы. Оно наблюдается в природе во всех диапазонах частот: от низких частот до микроволнового, инфракрасного, оптического, рентгеновского, диапазона гамма-излучения в физических процессах различного масштаба (от атомного до космического). Широко применяются искусственные источники излучения. В технике телекоммуникаций и измерительной технике широко используется излучение разнесенных в пространстве когерентных источников. Оно сопровождается формированием интерференционной картины в виде стационарного перераспределения интенсивности поля для волновых процессов любой физической природы. Расчет пространственного распределения интенсивности является классической задачей излучения в антенной технике акустических и электромагнитных источников и проводится в аналитическом виде обычно для неподвижных источников в изотропных средах [1-2], в подвижных средах [3,4], численно для более сложных конфигураций [5,6].
Вместе с тем, модель неподвижных источников является частной, идеализированной конструкцией, в реальных структурах и средах необходим учет подвижности источников излучения, играющей существенную роль во всех волновых процессах, в том числе и в наиболее важных для практики процессах интерференции и дифракции.
Целью работы является исследование изменения картины интерференции волн, создаваемых когерентными источниками в новых условиях – вращения системы излучателей.
Объектом исследования является процесс наложения волн излучаемых системой двух когерентных излучателей в ранее не рассматривавшемся, но важном для практики случае влияния на картину интерференции равномерного вращения системы когерентных излучателей, используемых при анализе и проектировании антенн различных частотных диапазонов.
Метод исследования – электродинамический анализ математической модели физического процесса интерференции волн, создаваемых системой когерентных источников.
Интерференция от неподвижных источников
Рассмотрим картину интерференции двух неподвижных когерентных источников, расположенных на расстоянии 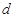 друг от друга и расстоянии
друг от друга и расстоянии 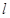 от экрана. Сложение волн с однонаправленными колебаниями в точке экрана Р (рис.1) описывается уравнениями:
от экрана. Сложение волн с однонаправленными колебаниями в точке экрана Р (рис.1) описывается уравнениями:
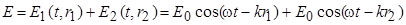 ,
,
где 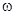 – частота,
– частота, 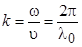 – волновое число,
– волновое число, 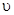 – скорость распространения волн,
– скорость распространения волн, 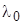 – длина волны. Условие максимума для разности хода
– длина волны. Условие максимума для разности хода 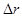 при сложении когерентных волн имеет вид:
при сложении когерентных волн имеет вид:
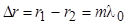 ,
,
где 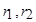 – оптическая длина пути первой и второй волн,
– оптическая длина пути первой и второй волн, 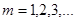 – номер максимума.
– номер максимума.
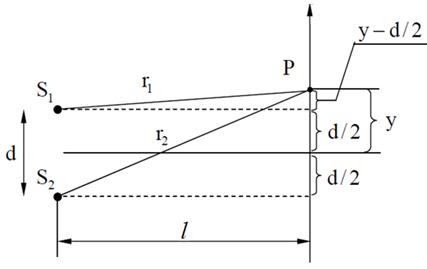
Рис.1. Суперпозиция волн от системы неподвижных когерентных источников
На экране наблюдается стационарное положение максимумов
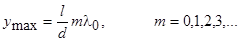 ,
,
и минимумов
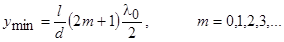 .
.
Расстояние между любыми соседними минимумами и максимумами одинаковое, ширина полос равна:
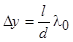 .
.
Вращение когерентных источников
Рассмотрим здесь распределение поля, создаваемого вращающейся системой двух зарядов (рис.2) в среде, характеризуемой скоростью распространения волн 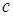 . В этом случае условия интерференции нарушаются.
. В этом случае условия интерференции нарушаются.
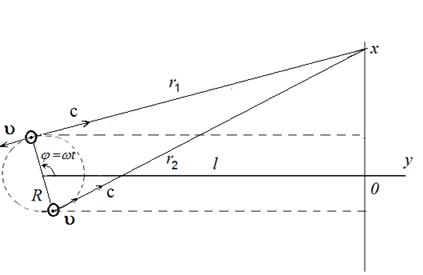
Рис.2. Суперпозиция волн от системы подвижных источников
Условия минимумов и максимумов становятся зависящими от времени. Причем, из-за эффекта Доплера, связанного с движением источников, нарушается условие когерентности 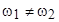 .
.
Частота излучения, фиксируемая в точке наблюдения P (рис.2) от каждого источника определяется соотношением [4]:
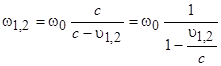 ,
,
где 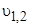 – скорости волн от первого и от второго источников излучения.
– скорости волн от первого и от второго источников излучения.
Проекции векторов скоростей волн, создаваемых вращающимися источниками излучения на направление точки наблюдения определяются соотношениями
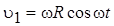 ,
,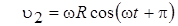 .
.
Движение излучателей приводит к эффекту:
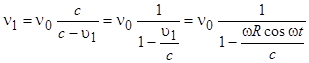 ,
,
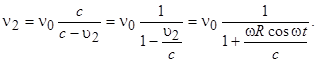
Это означает, что вращение когерентных источников приводит к нарушению когерентности сигналов этих источников во всех точках пространства. Зависимость изменения частот складываемых сигналов показана на рис. 3.
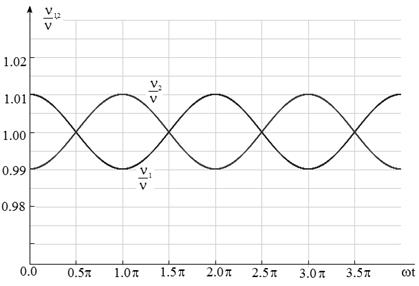
Рис. 3. Модуляция частот сигналов при вращении системы источников
Таким образом в точке P наблюдается периодическое изменение частот складываемых сигналов одновременно в сторону увеличения (создаваемого приближающимся источником) и в сторону уменьшения (удаляющимся в это же время источником).
Разность фаз складываемых волн когерентных источников определяется оптической разностью хода волн от двух источников и разностью фаз, связанной с нарушением когерентности из-за движения источников и равна
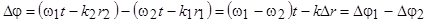 ,
,
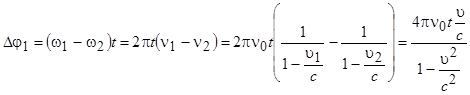 ,
,
где 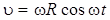 – проекция вектора скорости движения источника на направление точки наблюдения. Разность фаз за счет эффекта Доплера теперь зависит от времени.
– проекция вектора скорости движения источника на направление точки наблюдения. Разность фаз за счет эффекта Доплера теперь зависит от времени.
Кроме того, движение зарядов приводит к зависимости от времени и оптической разности хода лучей от источников 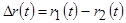 и соответственно разности фаз
и соответственно разности фаз 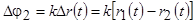 .
.
При этом расстояния от источников до точки наблюдения могут быть представлены в виде:
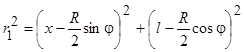 ,
,
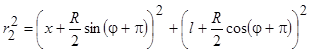 ,
,
где 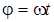 ,
, 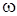 – частота вращения когерентных источников.
– частота вращения когерентных источников.
Для нахождения геометрической разности хода лучей найдем
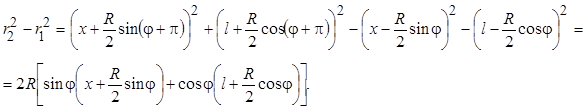
Учитывая, 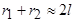 ,
, 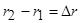 , геометрическая разность хода
, геометрическая разность хода
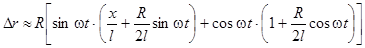 .
.
Разность хода, таким образом, зависит от времени, от частоты вращения системы когерентных источников. Разность фаз
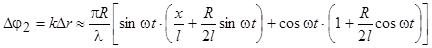 .
.
Учет обоих факторов дает соотношение
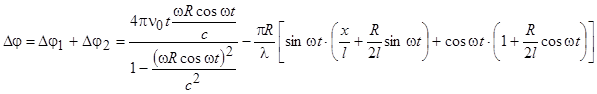 .
.
Обычно скорость движения источников 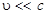 . В этом случае вклад эффекта Доплера в нарушение когерентности маленький и
. В этом случае вклад эффекта Доплера в нарушение когерентности маленький и 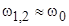 . Основной вклад в нарушение картины интерференции связан с перемещением источников и изменением разности хода лучей от источников до точки наблюдения
. Основной вклад в нарушение картины интерференции связан с перемещением источников и изменением разности хода лучей от источников до точки наблюдения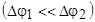 .
.
Эффект Доплера становится существенным в изменении картины интерференции при скоростях вращения 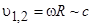 .
.
В соответствии с принципом суперпозиции, суммарное поле в любой точке пространства 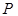 определяется суммой полей, создаваемых каждым источником:
определяется суммой полей, создаваемых каждым источником:
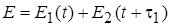 ,
,
где 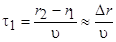 ,
, 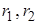 – расстояния от источников до точки наблюдения.
– расстояния от источников до точки наблюдения.
Интенсивность сигнала пропорциональна квадрату амплитуды напряженности электрического поля:
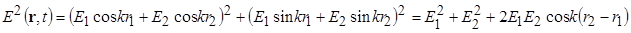 . Интенсивность волнового процесса:
. Интенсивность волнового процесса:
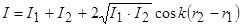 .
.
Фаза результирующего колебания:
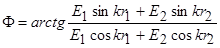 ,
,
где
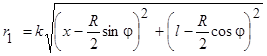 ,
,
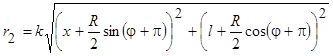 .
.
Максимальная интенсивность
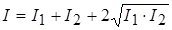
будет наблюдаться в тех точках, для которых выполняются соотношения:
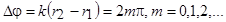 .
.
При равной интенсивности излучения обоих источников 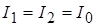 имеем:
имеем:
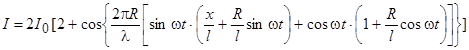 .
.
На рис.4 показана зависимость разности фаз в точке наблюдения от времени, определяющая характер зависимости от времени интенсивности волнового процесса
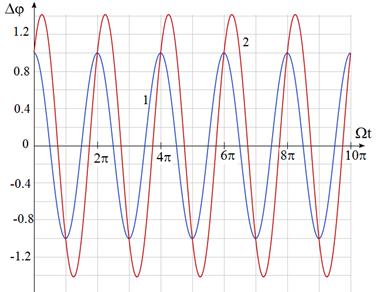
Рис.4. Временная зависимость разности фаз от скорости вращения
системы излучателей (1- 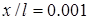 , 2-
, 2-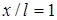 )
)
Полученные соотношения позволяют рассчитать распределение интенсивности и фазы результирующего колебания в произвольной точке пространства при любом пространственном расположении источников.
Вращение источников формирует амплитудную модуляцию интерференционной картины, создаваемой когерентными источниками с частотой модуляции равной частоте вращения. С ростом скорости вращения растет частота модуляции.
Она зависит как от положения точки наблюдения Р, так и от времени. В каждой точке пространства наблюдается модуляция интенсивности излучения с частотой вращения 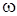 системы двух излучателей.
системы двух излучателей.
Заключение
Вращение системы когерентных источников приводит к нарушению когерентности волн в любой точке пространства и стационарная картина интерференционного распределения интенсивности нарушается.
В каждой точке пространства наблюдается модуляция амплитуды интенсивности и модуляция частот волн источников с частотой вращения источников. Это необходимо учитывать при расчете диаграммы направленности излучателей подвижных антенных систем, что имеет большое практическое значение.
 science-review.ru
science-review.ru