Введение. Классическая теория электромагнитного поля (ЭМП), базирующаяся на решениях системы уравнений Максвелла, предназначена для описания макрообъектов. Система уравнений Максвелла решается относительно электродинамических потенциалов, которые связаны с силовыми характеристики электромагнитного поля:
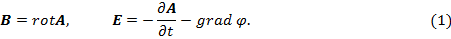
Характеристики поля 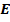 и
и 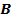 инвариантны по отношению к преобразованиям потенциалов, что позволяет наложить на потенциалы ЭМП дополнительные условия, предназначенные для устранения некоторого произвола для искусственно введенных потенциалов
инвариантны по отношению к преобразованиям потенциалов, что позволяет наложить на потенциалы ЭМП дополнительные условия, предназначенные для устранения некоторого произвола для искусственно введенных потенциалов 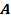 и
и 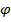 , а выбор типа калибровочных соотношений диктуется добством решаемой задачи.
, а выбор типа калибровочных соотношений диктуется добством решаемой задачи.
В теории ЭМП используются два типа калибровочных соотношения [1]: калибровка Лоренца и кулоновская калибровка 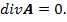
Кулоновская калибровка разделяет поле на две составляющие: поперечную, описываемую потенциалом 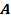 , и продольную, описываемую потенциалом
, и продольную, описываемую потенциалом 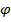 .
.
Уравнения для потенциалов в вакууме при кулоновской калибровке:
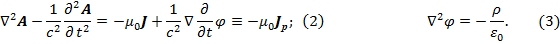
Скалярный потенциал 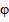 определяется мгновенным распределением зарядов так, как будто заряды покоятся. Классические выражения для потенциала
определяется мгновенным распределением зарядов так, как будто заряды покоятся. Классические выражения для потенциала 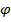 и продольного тока
и продольного тока 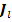 соответственно представляются выражениями:
соответственно представляются выражениями:
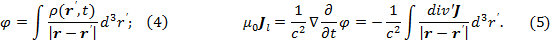
В [2] утверждается, что в правой части (2) останется только результирующая – поперечная составляющая тока 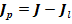 , которая не всегда очевидна.
, которая не всегда очевидна.
Пусть источником ЭМП является движущийся со скоростью 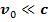 точечный заряд
точечный заряд 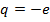 с объемной плотностью
с объемной плотностью 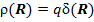 , где
, где 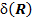 – дельта функция;
– дельта функция; 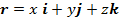 и
и 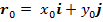 – радиус-векторы неподвижной точки и заряда в неподвижной системы отсчета;
– радиус-векторы неподвижной точки и заряда в неподвижной системы отсчета; 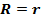 –
–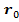 – вектор, соединяющий центр заряда с неподвижной точкой.
– вектор, соединяющий центр заряда с неподвижной точкой.
Выразим ток 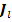 через напряженность кулоновского поля
через напряженность кулоновского поля 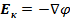 , то проявится природа продольного тока - обусловлен движением кулоновского поля:
, то проявится природа продольного тока - обусловлен движением кулоновского поля:
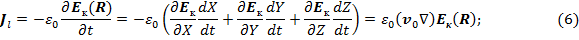
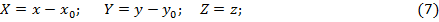
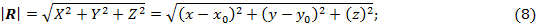
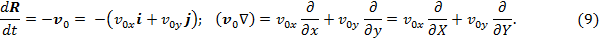
Цель исследования. Изучим свойства волнового уравнения (2) с током (6).
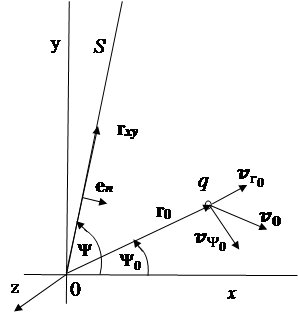 Метод интегрирования волнового уравнения векторного потенциала. Пусть (2) описывает поле электрона, вращающегося в центрально-симметричном электростатическом поле (рис 1), плоскость орбиты которого расположена в координатной плоскости OXY (
Метод интегрирования волнового уравнения векторного потенциала. Пусть (2) описывает поле электрона, вращающегося в центрально-симметричном электростатическом поле (рис 1), плоскость орбиты которого расположена в координатной плоскости OXY (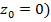 . Начало системы координат совместим с центром центрально-симметричного поля.
. Начало системы координат совместим с центром центрально-симметричного поля.
Рис. 1. Относительное мгновенное расположение электрического заряда q и неподвижной плоскости S в системе координат, где 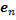 – единичный направляющий вектор плоскости,
– единичный направляющий вектор плоскости, 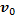 – вектор скорости заряда
– вектор скорости заряда
Запишем формулы электронной плотности тока 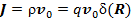 и электрической индукции кулоновского поля
и электрической индукции кулоновского поля 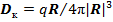 . Учитывая в (6) выражения (8) и (9), получим:
. Учитывая в (6) выражения (8) и (9), получим:
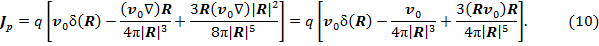
Распределения плотностей электронного 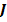 и кулоновского полевого
и кулоновского полевого 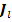 токов не тождественны, поэтому их воздействия можно оценивать по значениям силы тока. Для этого вычислим результирующую силу тока через неподвижную полуплоскость
токов не тождественны, поэтому их воздействия можно оценивать по значениям силы тока. Для этого вычислим результирующую силу тока через неподвижную полуплоскость 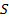 (ток заряда, движущегося по замкнутой траектории, рассчитывается в одной точке пересечения траектории с поперечной плоскостью). Пусть полуплоскость перпендикулярна плоскости орбиты и проходит через ось
(ток заряда, движущегося по замкнутой траектории, рассчитывается в одной точке пересечения траектории с поперечной плоскостью). Пусть полуплоскость перпендикулярна плоскости орбиты и проходит через ось 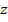 и неподвижный радиус вектор
и неподвижный радиус вектор 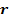 (с азимутальной координатой
(с азимутальной координатой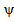 ). Мгновенный ток, создаваемый одиночным орбитальным точечным зарядом, усредним за время
). Мгновенный ток, создаваемый одиночным орбитальным точечным зарядом, усредним за время 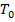 , равное периоду вращения. При этих условиях (2) будет иметь вид:
, равное периоду вращения. При этих условиях (2) будет иметь вид:
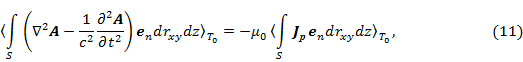
где символом 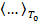 обозначен оператор усреднения по времени за период
обозначен оператор усреднения по времени за период 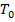 , а пределы интегрирования соответственно равны: по
, а пределы интегрирования соответственно равны: по 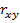
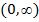 ; по
; по 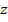
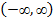 ,
, 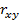 – проекция
– проекция 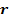 на координатную плоскость OXY. Единичный нормальный к неподвижной плоскости
на координатную плоскость OXY. Единичный нормальный к неподвижной плоскости 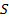 вектор
вектор 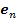 направим в сторону движения заряда
направим в сторону движения заряда 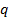 :
:
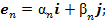
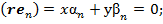
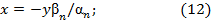
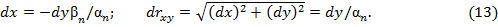
Вычислим в три этапа правую часть уравнения (11) с учетом (10).
1) В первом слагаемом (10) с током 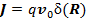 выразим
выразим 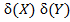 в полярных координатах [], то
в полярных координатах [], то 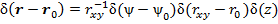 , где
, где 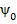 ,
, 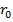 – полярные координаты заряда, то формула силы электронного тока примет вид:
– полярные координаты заряда, то формула силы электронного тока примет вид:
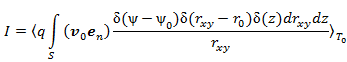
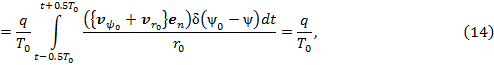
где учли: 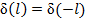 ;
; 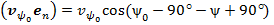 согласно рис.1;
согласно рис.1; 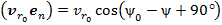 и
и 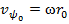 ,
, 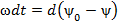 ,
, 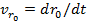 ;
;
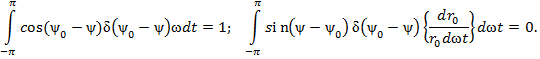
2) Силу тока от второго слагаемого (10) определим при помощи табличного интеграла [3, с. 92], использовав (13) и обозначив 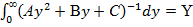 :
:
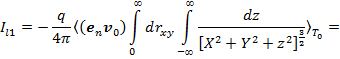
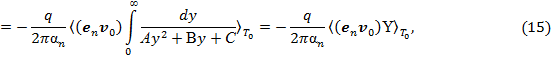
Постоянные коэффициенты в (16) получены на основе (7) и (12):
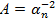 ;
; 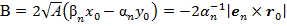 ;
; 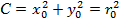 ,
, 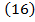
3) Силу тока от третьего слагаемого (10) определим при помощи табличных интегралов [3, с. 92; с. 36], (см. Приложение). Учитывая 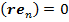 и в соответствии с (12)
и в соответствии с (12) 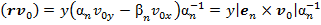 , получим:
, получим:
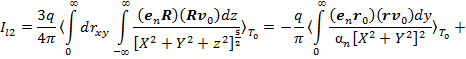
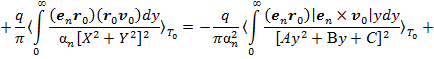
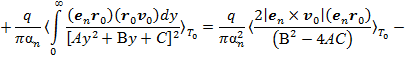
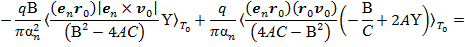
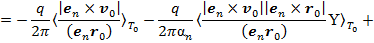
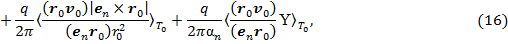
где в последних выражениях на основе (12), использовали следующее представление:
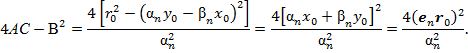
Обозначив 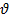 угол между
угол между 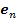 и
и 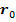 и учтя следующие преобразования
и учтя следующие преобразования
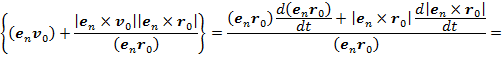
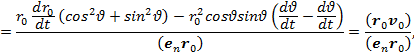
сумма токов (15) и (16) примет следующий вид:
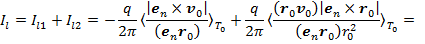
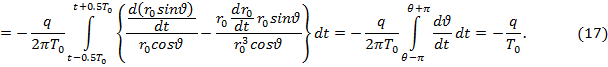
На основе (14) и (17) результирующая сила тока 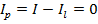 .
.
Результаты. Получено важное научное положение, что усредненные за период движения заряда по замкнутой произвольной стационарной орбите электронный ток компенсируется кулоновским полевым током. Это означает то, что в классическом приближении отсутствует физическая причина излучения электромагнитной энергии зарядом, вращающимся на стационарной (замкнутой) орбите.
Поменяв порядок интегрирования, уравнение (11) относительно проекции векторного потенциала 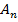 на направление
на направление 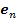 примет следующий вид:
примет следующий вид:
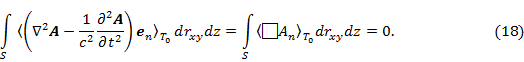
В исследуемой задаче ЭМП поле слева и справа от плоскости орбиты симметрично, то отсутствие потока вектора 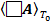 (где
(где 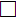 – волновой оператор) через произвольную полуплоскость (нормальной к плоскости орбиты) возможно, если подынтегральное выражение (18) будет равно нулю. Поэтому в силу линейности оператора усреднения одно из решений (18) примет следующий вид:
– волновой оператор) через произвольную полуплоскость (нормальной к плоскости орбиты) возможно, если подынтегральное выражение (18) будет равно нулю. Поэтому в силу линейности оператора усреднения одно из решений (18) примет следующий вид:
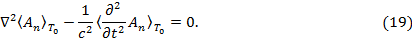
Уравнение (19) – однородное волновое уравнение, в котором отсутствует источник воздействия, поэтому это уравнение описывает стационарный (в соответствии с исходными условиями задачи), но непринужденный волновой процесс ЭМП [4]. Такому условию соответствуют незатухающие колебания ЭМП с собственной частотой 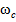 , которая физически связана с орбитальным движением электрона, но
, которая физически связана с орбитальным движением электрона, но 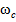 может не совпадать с частотой его вращения
может не совпадать с частотой его вращения 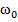 : положим связь
: положим связь
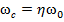 . (20)
. (20)
Задавая для 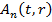 первообразную
первообразную 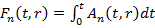 , имеем
, имеем 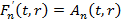 , на основе которого получим остальные производные:
, на основе которого получим остальные производные:
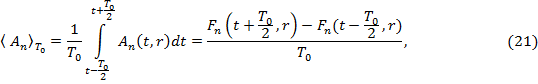
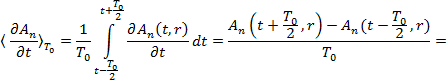
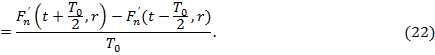
Дифференцируя по времени (21) и подставляя (22), получим
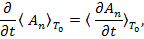
и аналогично

Будем искать решения однородных уравнений (19) с учетом (21) и (23) в виде произведения двух комплексных функций:

тогда, подставив (24) в (23) и (19), получим
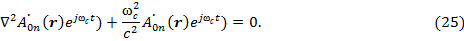
Для стационарного процесса достаточно в формулах усреднения (21) – (23) положить первый период обращения электрона вокруг ядра (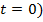 . Поэтому волновое уравнение для усредненного стационарного процесса примет вид уравнения Гельмгольца [5]:
. Поэтому волновое уравнение для усредненного стационарного процесса примет вид уравнения Гельмгольца [5]:

В случае круговой орбиты с радиусом 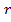 вращения электрона в центрально-симметричном силовом поле протона частота вращения описывается известной формулой
вращения электрона в центрально-симметричном силовом поле протона частота вращения описывается известной формулой 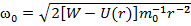 , где
, где 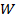 ,
, 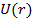 – соответственно полная и потенциальная энергии электрона,
– соответственно полная и потенциальная энергии электрона, 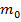 – его масса [6]. Запишем коэффициент в уравнении (26) с учетом (20) в следующем виде:
– его масса [6]. Запишем коэффициент в уравнении (26) с учетом (20) в следующем виде:

Теперь потребуем, чтобы уравнение (26) удовлетворяло научно обоснованному условию – чтобы стационарные орбиты электрона были квантованы. Уравнение (26) с учетом (27) может удовлетворить этому требованию, если приравнять к постоянной Планка 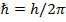 знаменатель выражения (27):
знаменатель выражения (27):

При условии (28) уравнение (26) по структуре становится полностью подобным стационарному уравнению Шредингера [6], решение которого в центрально-симметричном силовом поле для атома водорода широко известно и ему соответствует дискретный спектр полной энергии 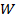 электрона в центрально-симметричном поле протона. Поэтому решение однородного уравнения (26) – (28) в сферическом базисе принимает аналогичный вид
электрона в центрально-симметричном поле протона. Поэтому решение однородного уравнения (26) – (28) в сферическом базисе принимает аналогичный вид

где 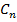 – нормировочный коэффициент,
– нормировочный коэффициент, 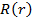 – радиальная функция,
– радиальная функция, 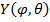 – сферическая функция.
– сферическая функция.
Решению (29) соответствует дискретный спектр собственных частот (27) колебаний ЭМП. Выражая радиусы  дискретных орбит электрона через радиус Бора
дискретных орбит электрона через радиус Бора 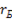 :
: 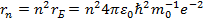 (
(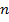 – номер стационарной орбиты,
– номер стационарной орбиты, 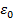 – электрическая постоянная) и, подставляя в (28), раскрываем физическое содержание введенного в (20) коэффициента связи
– электрическая постоянная) и, подставляя в (28), раскрываем физическое содержание введенного в (20) коэффициента связи

где 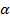 – совпадает с постоянной тонкой структуры, а
– совпадает с постоянной тонкой структуры, а 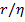 =
= 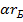 = const [6]. Далее из (27) – (29) с учетом выражения
= const [6]. Далее из (27) – (29) с учетом выражения 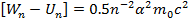 собственные частоты колебаний ЭМП в атоме определяются формулой:
собственные частоты колебаний ЭМП в атоме определяются формулой: 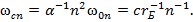
Так как 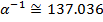 иррациональное число, то
иррациональное число, то 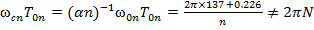 , где
, где 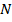 - целое число, то при исходных допущениях
- целое число, то при исходных допущениях 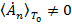 .
.
Заключение.
1. К существующим понятиям (электронный ток и ток смещения) добавлен еще один вид тока, обусловленного перемещением кулоновского электрического поля (назовем кулоновским полевым током).
2. Для движущихся электрических зарядов (электронов) по стационарным замкнутым орбитам произвольной формы (окружность, эллипс) в среднем за период вращения электронный ток каждого заряда компенсируется кулоновским полевым током. Это означает, что в классическом приближении раскрыта физическая причина отсутствия излучения электромагнитной энергии вращающимися электронами в атоме [7].
3. Усредненное за время одного оборота волновое уравнение относительно проекции векторного потенциала на нормаль к неподвижной полуплоскости становится однородным и допускает решение, подобное решению стационарного уравнения Шредингера для атома водорода. Это означает, что классическое приближение разрешает движение электрона в центрально-симметричном силовом поле только по дискретным орбитам: квантование орбит.
Приложение. Значения интегралов, проверенных дифференцированием их неопределенных интегралов [3, с. 92 №17 и №9; с. 36 №22 и №17]:
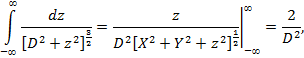
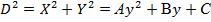
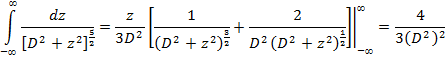
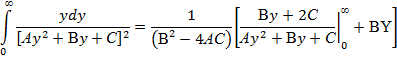
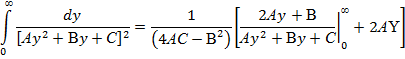
 science-review.ru
science-review.ru