Цель исследования
Целью исследования был поиск решения полиномов с комплексными коэффициентами (для малых степеней полиномов), а также возможных решений для полиномов с целыми степенями n>4.
Вычисления над комплексными числами (т.е. числами, состоящими из действительной и мнимой частей) будут всё сильнее влиять на точные науки, в том числе и на космологию.
Можно, например, предположить, что и так называемая тёмная материя может представлять собой некую «мнимую» величину(материю) относительно видимой части вселенной по координате времени. Ведь не могут тела во вселенной воздействовать мгновенно. Для этого необходимо некоторое время, которое для нас представляется в виде темной материи (точнее, некой силой, проявляющей себя как темная материя). И можно предположить, что со временем комплексные величины будут всё сильнее влиять на все наши вычисления, ведь если некоторые параметры имеют мнимые составляющие, то сочетания таких комплексных величин могут дать ощутимую прибавку (или убыль) из-за мнимых составляющих.
В математике мнимые величины повсеместно проявляются при вычислениях полиномов[1-6]. Как известно, при решении квадратного уравнения (полинома второй степени), как и любого полинома чётной степени, корни с комплексными величинами могут появиться даже при действительных коэффициентах. Также решение квадратного уравнения возможно с комплексными коэффициентами, в отличие от решения кубического полинома, которое, как известно, решается с помощью формулы Кардано [1]. В источниках по поводу решения данной формулой указывается, что коэффициенты должны быть только действительными. Таких ограничений на коэффициенты нет при варианте, рассматриваемом ниже (решения находятся при любых комплексных коэффициентах). Итак, если в кубическом полиноме
y3 + a1 y2 + a2 y + a3 = 0 (1)
выполняется следующее соотношение коэффициентов:
a12 - 3 a2 = 0 (2)
то переписав уравнение (1) так:
y3 + 3 a1/3 y2 + 3 (a1/3)2 y + (a2 - a12/3) y + a3 = 0
видим, что условие (2) приводит к простому решению полинома:
(y + a1/3)3 = a13/27 - a3
И только при невыполнении условия (2), было найдено ещё одно решение кубического полинома, но уже с любыми комплексными коэффициентами:
a12 - 3 a2 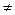 0
0
переходим к подстановке :
y = x + k
После перехода к промежуточному корню x и делением на куб, полином преобразуется к виду:
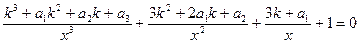
Теперь в этом уравнении делим все члены на числитель первого члена и применяем подобие условия (2), т.е. здесь условие (2) обеспечивает некая неизвестная величина k:
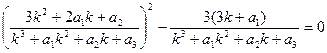
Решая это выражение, получаем квадратное уравнение относительно величины k :
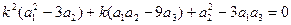
Значение k будет :
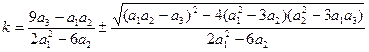
Теперь выражение для нахождения промежуточного корня x будет таким:
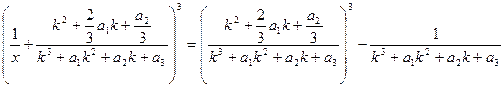
Отсюда находим x – из:
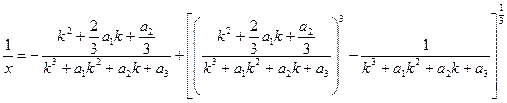
а затем и корень y = x + k.
В случае
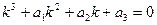
получаем квадратное уравнение относительно величины x.
Решение полинома 4-й степени, приведенное в [6], возможно также с любыми комплексными коэффициентами. Решение же полиномов со степенью, большей 4, как известно, в общем виде не существует. Ниже будет рассмотрен итерационный способ решения таких полиномов, но с действительными коэффициентами. Итак, пусть имеется полином некой степени n с действительными коэффициентами:
F(y) = yn + c1yn-1 + c2yn-2 + c3yn-3 + … + cn-1y + cn = 0 (3)
Получение корня будет итерационным с использованием по возможности способов минимизации вычислений (уменьшения числа итераций). Для начала рассмотрим способ получения корня полинома любой нечетной степени. Для четной степени будет рассмотрено ниже.
Конечно, корень следует искать внутри всего диапазона действительных чисел: от -∞ до +∞. Однако, как было выяснено, корень с максимальным значением не выходит за границу
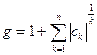
Поэтому достаточно просмотреть 4 диапазона (вычисляя остатки F(y) на границах):
[-g , -1] , [-1 , 0] , [0 , 1] , [1 , g]
Т.е. на границах gi = -g, -1, 0, 1, g
Для полинома нечетной степени обязательно найдется диапазон, где граничные остатки F(y=gi) и F(y=gi+1) имеют разные знаки. В этом диапазоне и будет хотя бы один корень.
Диапазонов с разными знаками на границах может быть и не одно, в этом случае лучше взять диапазон с наименьшей разницей расхождения. Пусть это будет диапазон с граничными остатками (с противоположными знаками) Fu(c начальным – итерационным - значением границы gi = ru) и Fv (gi+1 = rv).
Для получения следующего итерационного значения, ведущего к корню, используем следующее выражение:
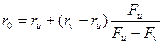 (4)
(4)
Может так случиться, что в некоторых случаях граничных значений Fu или Fv величина r0 может выйти за диапазон ru, rv. В это случае делаем проверку, предварительно используя некую величину w. И при значении Fu < 0, Fv > 0, но rv < ru, берем w = -1, иначе w = 1.
Теперь, в случае если
r0 * w < ru * w , либо r0 * w > rv * w (5)
- это вариант выхода за границы, берем
r0 = ( ru + rv ) / 2
где ru , rv граничные значения(-g,-1,0,..), и Fu = F(ru), Fv - их остатки (один со знаком плюс, другой – со знаком минус).
Полученное значение r0 может сразу привести в область корня и(или) позволяет, по его остатку F(r0) – знаку остатка, сузить область нахождения корня. Теперь, можно было бы в соответствии знака остатка F(r0), заменить значения ru,Fu (либо rv,Fv) в формуле (4) и получить новое приближение к корню полинома (3), до F(r0)=0, что означает нахождение корня y = r0 . Но, как показали вычисления, это ведет к медленной сходимости к корню. Был найден путь, который приводит к корню быстрее. Итак, заменяем в соответствии полученного значения –знака остатка- F(r0) величину Fu , либо Fv .
Для получения следующего итерационного цикла вычисляем некую величину m = | Fu / Fv |
т.е. соотношение граничных остатков по абсолютной величине. Для оптимальных вычислений были выбраны ограничения: при m > 12 , берем m = 10 ; при m < 1/12 берем m = 0.1
Вычисляем новое значение приближения к корню:
r1 = [ ru * (1 + 1/m) + rv*(1 + m) ] /(2 + m + 1/m)
Отсюда получаем новый остаток F(r1), которым заменяем, в зависимости от знака, Fu или Fv.
Теперь используем и 3-й, последний этап вычисления в итерационном цикле (состоящий из 3-х этапов, дающих ускоренное приближение к корню). Итак, берем знаки полученных остатков F(r0) и F(r1):
s0 = sgn(F(r0)), s1= sgn(F(r1))
где s0 и s1 принимают одно из 3-х значений: -1, 0, 1. При значении 0 корень считается найденным и равным соответственно r0, либо r1.
При ненулевых значениях остатков берем сумму s = s0 + s1. И если она по абсолютной величине равна 2 (т.е. при остатках по одну сторону от 0 - с одинаковым знаком), то вычисляем
r0 = [ru * (s/4+ 3/2) +( -s/4+3/2) * rv] / 3 (6)
Т.е. в этом случае вполне можно взять не половину области, а только третью часть. И переходим к проверке (5). В случае s = 0, т.е. остатки F(r0) и F(r1) имеют разные знаки, переходим к вычислению значения по формуле (4). И т.д.
В принципе можно в промежуточных частях, очевидно, брать и некоторые другие разбиения искомой области, однако, можно получить, как ускорение перехода к корню, так и замедление.
Теперь о полиноме чётной степени с действительными коэффициентами.
Здесь имеется 2 варианта : n = 4k + 2 и n = 4k, где k = 1, 2, 3,..
Из полинома (3) получаем 2 полинома
P1(y) = y2k+1 + c1y2k + c2y2k-1 + c3y2k-2 + … + c2ky + c2k+1 = 0
P2(y) = c2k+2/y + c2k+3/y2 + c2k+4/y3 + … + cn-1/yn-2k-2 + cn/yn-2k-1 = 0
Для работы нам потребуется составной как бы «нечетный» полином: P(y) = P1(y) + P2(y)
Кстати, P(y)*yn-2k-1 = F(y) .Также вычисляем некую величину g:
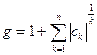 (7)
(7)
Которая будет находиться вблизи значения вероятного максимального корня.
Теперь всю область действительных чисел разбиваем на 3 части:
[-g , -1] , [-1 , 1] , [1 , g] (8)
В чётном полиноме с действительными коэффициентами могут быть корни и с действительными значениями, и с комплексными значениями (с мнимой составляющей), которые попарно составляют сопряженные значения корней :
y1 = rd + i*rm , y2 = rd – i*rm (9)
и образуют (и вводят в полином ) квадратное уравнение без мнимой составляющей:
y2 + v1*y + v2 = 0
где v1 = -2*rd , v2 = rd2 + rm2 .
В общем, уравнение (3) теперь можно представить в виде
F(yn) = F(yn-2) * (y2 + v1 * y + v2) = 0
Случай, если v2 не имеет комплексной составляющей, является частным и также находится по приведенному ниже способу. Для начала граничные значения (8) применим к полиному P(y) – т.е. находим остатки P(gi), где gi = -g, -1, 1, g.
У нас возможны либо 1, либо 3 варианта смены знака (+-) на границах областей. Остаток P(-g) будет всегда иметь отрицательный знак, P(g) – всегда положительный. При 3-х вариантах выбираем либо 1-ю область, либо 3-ю, там, где остатки образуют меньший разброс. И только при единственном варианте, когда смена знака происходит в средней области: [-1, 1], вместо P(y) будем использовать P1(y). В этом случае опять проверяем смену знаков остатков, только уже P1(y) на границах областей (8). Как правило, оно может указать на 1-у или 3-ю область в (8). И только, если снова будет указана средняя область, берем первую, т.е. [-g, -1].
Теперь мы подошли к получению начального значения rd. Его мы получаем по подобию нечетного полинома: уравнения (4) – (6).
После получения начального значения rd, если, вместо P(y), использовался P1(y), окончательное предварительное значение r0 вычисляем, используя в вычисленных точках ru, rv остатки P(ru), P(rv).
Будем считать, что начальное значение rd из уравнения (9) получено. Здесь может быть случай, что остаток P(rd) является достаточно малой величиной: например, если взять за критерий определения малости остатка величину g из (7), и остаток P(rd) будет на несколько порядков меньше этой величины g, то можно предположить, что, во-первых, корень скорее всего найден и находится вблизи значения rd, а во-вторых это действительный корень (нет мнимой составляющей). Если корень имеет мнимую составляющую, то, очевидно, остаток P(rd) будет далек от минимальных значений и критерий сравнения малости со значением g из (7) выполняться не будет. В этом случае переходим ко второму этапу нахождения корня(корней, в случае сопряжения ).
Получаем начальное значение v1 = -2*rd.
Теперь для примера, рассмотрим случай n = 6.
Для решения уравнение (3) предполагалось равным:
F(y) = (y2 + m1y + m2)*(y2 + m3y + m4)*(y2 + v1y + v2)
Получилась система из шести уравнений относительно неизвестных m1, m2, m3, m4, v1, v2.
При решении все mk определяются относительно коэффициентов ck.
В итоге остается система из 2-х уравнений, состоящая из искомых величин v1(= -2*rd) и v2 (= rd2+rm2) вместе с коэффициентами ck уравнения (3), которую можно представить в виде:
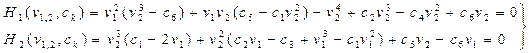 (10)
(10)
Из этой системы получаем выражение для нахождения v2:
v2(b1b32 - b2b3 + b3b4b5 - b52) = b2b5 - c6b32 - b2b3b4 (11)
где
b1 = c3v1 – c2v12 – v14 - c4 + c1v13 ; b2 = c1c6 – 3c6v1
b3 = 5v13 – 6c1v12 + v1(c2 + 2c12) – c1c2 + c3 ; b4 = c2 + 3v12 – 2c1v1
b5 = 2v15 – 3c1v14 + v13(c12 + 2c2) – v12(c1c2 + 2c3) + v1(c1c3 +2c4) - c1c4 + c5
Таким образом, получаем и начальное значение v2, благодаря которому мы можем получить следующее уточнённое выражение для v1, которое также можно получить из системы (10):
v1 = v2[(c6 - v23)(c1v25 - c3v24 + c5v23 - c1c6v22 + c3c6v2 - c5c6) + v22(c1c6 - c5v2)(c6 - v23 + c2v22 -c4v2)]/[(c6 - v23)(v26 - c4v24 + c2c6v22 - c62) + v23(c5v2 - c1c6)(c5 - c1v22)]
Обозначим это уточнённое значение как v1_1.
Итак, после получения на первом этапе начального значения v1, затем по формуле (11) значения v2, получается уточненное значение v1 = v1_1. В целом, в конечном итоге мы получим истинные значения v1 и v2. Но в начальных циклах итерации значения v1, v1_1 могут быть далеки от истинных значений v1. В общем, к дальнейшим вычислениям используем v1_2 = (v1 + v1_1)/2.
Теперь, подставляем в систему (10) сначала пару v1, v2 и получаем остатки H1, H2.
Суммируем эти 2 остатка по их абсолютным значениям: Z1 = | H1 | + | H2 |
Затем подставляем в систему пару v1_2, v2 и получаем другие остатки H1_1, H2_1.
Также получаем из них сумму их абсолютных значений: Z2 = | H1_1 | + | H2_1 |
И наконец, получаем знаки (+/-) сумм остатков: s1 = sgn(H1 + H2) ; s2 = sgn(H1_1 + H2_1)
где s1 и s2 могут принять одно из 3-х значений: -1, 0, 1.
Следующее итерационное значение v1 (=v1_3) определяется по 3-м вариантам:
В1. Если сумма s1 + s2 = 0, то v1_3 = (v1 + v1_2)/2
B2. При невыполнении условия B1, если Z2 < Z1, то v1_3 = v1_2
B3. Если не выполняются условия B1 и B2, то v1_3 = v1 + (v1_2 – v1) * Z1 / (Z1 – Z2)
Таким образом для получения конечных значений v1, v2 подставляем найденное v1, находим v2 , подставляем v2, находим уточненное v1 и т.д. Также можно на каждом этапе(цикле) производить проверку на величину остатка исходного уравнения (3). Т.е. , в очередном цикле находим rd и rm посредством промежуточных вычислений: получаем некие p1 = - v1_3/2; p2 = p12 – v2; r = ( | p2 | )1/2
Если p2 >= 0, то rd = p1 + r, rm=0 (и 2-й вариант: rd_2 = p1 – r; rm_2 =0) ; иначе rd = p1, rm = r ( 2-й вариант: rd_2 = p1; rm_2 = - r).
Теперь, имея в итерационном цикле вычисленные значения y1 = rd + i*rm и y2= rd_2 + i*rm_2
находим остатки F(y1) и F(y2) уравнения (3) для действительной части и мнимой:
так для действительной части F(y1) при n=6 получим:
F(y1)_d = rd6 - 15rd4rm2 + 15rd2rm4 – rm6 + c1(rd5- 10rd3rm2 + 5rdrm4) + c2(rd4- 6rd2rm2 + rm4) +
+ c3(rd3 - 3rdrm2) + c4(rd2 - rm2) + c5rd + c6
И для мнимой части:
F(y1)_mn == 6rd5rm - 20rd3rm3 + 6rdrm5 + c1(5rd4rm - 10rd2rm3 + rm5) + c2(4rd3rm - 4rdrm3) +
+ c3(3rd2rm - rm3) + c4(2rdrm) + c5rm
Также получаем и для F(y2). Для работы нам нужна сумма остатков абсолютных значений:
F1 = | F(y1)_d | + | F(y1)_mn | ; F2 = | F(y2)_d | + | F(y2)_mn |
Значения остатков могут привести к таким 2-м вариантам:
- одно из значений: F1 или F2 имеет довольно малую величину (например, на порядок меньше значения g – из (7), принятом критерием малости остатка). В этом случае можно считать, что найденные значения rd, rm находятся вблизи значения искомого корня. При rm=0 корень имеет действительное значение.
- значения F1 и F2 имеют примерно одинаковые значения и плавно уменьшаются от итерации к итерации. В этом случае корни, скорее всего комплексные и стоит продолжать итерационные циклы до получения, например, критерия малости остатка (остаток на порядок меньше величины g ).
Теперь, в случае не первого итерационного цикла, если остатки F1, F2 довольно большие, или v1 отличается от v1_3, например, на величину, большую в 7 %, вычисляем конечную в цикле величину v1 = (v1 + v1_3)/2 , иначе берем v1= v1_3. И переходим к вычислению величины v2 – уравнение (11), что будет означать переход на очередной итерационный цикл.
Дополнительно можно делать анализ на приближение к корню y (=rd+irm) - значений y1 и y2, переходящие от цикла к циклу, и если их разность, например, будет меньше какой либо малой величины(например 10-5), то тоже можно принять, что корень найден.
Таким же способом можно составить подобие системы (10) и для n = 8 для нахождения корня полинома 8-й степени и т.д.
Также для полинома 5-й степени с действительными коэффициентами есть ещё один способ числового итерационного решения через полином 3-й степени. Итак, представим полином 5-й степени таким образом:
y3 + a1 y2 + a2 y = - a3 – a4/y – a5/y2 (12)
И для ускоренного решения «обратное» :
1/y3 + (a4/a5) 1/y2 + (a3/a5) 1/ y = - a2/a5 – (a1/a5) y – y2/a5 (13)
Здесь в правые части уравнений (12) и (13) будем ставить приближённые значения y0.
Так начальное значение y0 для уравнения (12) находим следующим способом:
Получаем некие g1 и g2:
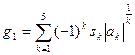
где здесь и далее sk – это знак коэффициента ak, принимающий значение -1, 0, +1.
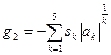
Теперь при условии
[ s(g1) + s(g2)]/( – s5 ) = 2 (14)
где здесь и далее s(g1) – это знак числа g1, s(g2) – знак числа g2 ,
получаем начальное значение y0 = ( g1 + g2 )/2
При невыполнении условия (14), проверяется условие равенства s(g1) = - s5. При выполнении этого условия берем y0 = g1, иначе y0 = g2.
Решаем полином 3-й степени, исходя из уравнения (12):
y3 + a1 y2 + a2 y = - a3 – a4/y0 – a5/y02 (15)
где получаем 3 корня.
Примерно таким же способом ищем начальное значение (пусть y1) для уравнения (13):
Снова получаем некие g1 и g2
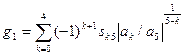
где sk5 – это знак дроби коэффициентов: ak/a5, a0 = 1
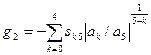
Теперь также находим начальное значение y1 из условий: при ( s(g1) + s(g2))/( – s5 ) = 2
значение y1 = 2/ (g1 + g2)
При невыполнении этого условия проверяем равенство s(g1) = - s5 и если оно имеет место, то берем y1 =1/ g1, иначе y1 =1/ g2.
Также решаем «обратный» полином 3-й степени:
1/y3 + (a4/a5) 1/y2 + (a3/a5) 1/ y = - a2/a5 – (a1/a5) y1 – y12/a5 (16)
Отсюда получаем некий корень 1/y (точнее 3 корня) , где в знаменателе следующее приближение корня y2.
Теперь, получив ближайшие по значению приближения - из уравнений (15) и (16), можно определить следующее приближенное значение корня этого итерационного цикла: пусть из уравнения (15) приближенным значением является некая величина y01, из (16) некая величина y02, тогда при условии [ s(y01) + s(y02) ]/(- s5) = 2 , где s(y01) и s(y02) – это знаки чисел y01 и y02 , получаем следующее приближение y3 = ( y01 + y02 )/2 , при невыполнения условия проверяем равенство s(y01) = - s5, и если оно выполняется, то y3 = y01, иначе y3 = y02.
Проверяем остаток полинома F(y = y3) по формуле (3). И если он достаточно мал, то считаем, что корень находится вблизи значения y3. В противном случае переходим к очередному итерационному циклу определения корня по уравнениям (15) и (16).
 science-review.ru
science-review.ru