Введение. Исходя из практических задач анализа информационных моделей, был введен т.н. обобщенный пропозициональный язык, который получается расширение области определения обычных логических связок на счетные аргументы [1]. Такой язык обладает различными интересными семантиками, и оказывается полезным при решении различных прикладных задач, в том числе связанными с анализом вычислительных моделей [2, 3, 4]. Однако, если не вводить ограничений на обобщенные логические связки, то получается язык с весьма богатыми выразительными возможностями. Но именно поэтому его трудно применять для получения реальных результатов, касающихся вычислимых функций. Поэтому такой язык не представляет интереса в силу ограниченности его применения. С другой стороны, если ввести достаточно естественные ограничения на бесконечные связки, удается получить ограниченный язык т.н. примитичных формул с интересными свойствами, которые описаны в настоящей статье. С этой целью вводится понятие представления вычислимых функций обобщенными формулами. Двоичная функция y = f(x) представима обобщенной формулой F(x, y), если для каждой пары значений sx, sy соответственно аргумента и значения функции f равенство sy = f(sx) выполняется тогда и только тогда, когда формула F(sx, sy) истинная. В статье показывается, что все функции арифметики Пребургера представимы примитивными формулами обобщенного языка.
1. Представление вычислимых функций обобщенными формулами. Исходя из практических соображений, в множестве обобщенных формул, определенных в [1], выделено семейство примитивных формул, обладающих относительно простыми ограничениями на бесколнечные логические связки. В этом разделе исследуем выразительные возможности примитивного языка. С этой целью покажем, что с помощью примитивных формул можно описывать свойства некоторых функций двоичной арифметики.
При обозначении двоичных чисел младшие разряды будем располагать слева. Поэтому вектор s, представляющий двоичное число, содержит ненулевыми лишь конечное число левых разрядов. Все разряды, расположенные справа от самого правого единичного – нулевые. Таким образом, если бесконечный вектор обозначает двоичное число, то он имеет бесконечный нулевой суффикс.
Будем говорить, что логическая формула F(x1, x2, …, xn, y) представляет двоичную функцию y = f(x1, x2, …, xn), если при означивании переменных x1, x2, …, xn, y соответственно бинарными векторами s1, s2, …, sn, sn+1 формула F(s1, s2, …, sn, sn+1) истинна тогда и только тогда, когда f(s1, s2, …, sn) = sn+1. Отметим, что формула F(x1, x2, …, xn, y) может содержать и другие переменные, кроме указанных. Назовем их рабочими.
Просто доказывается следующая лемма.
Лемма 1.1. Если формула F(x1, x2, …, xn, y) представляет функцию f(x1, x2, …, xn) двоичной арифметики, то д-эквивалентная ей формула G(x1, x2, …, xn, y) также представляет эту функцию.
Пример 1.1. Обозначим x, y, z наборы двоичных переменных соответственно: x0, x1, …, xn,… ; y0, y1, …, yn,… и z0, z1, …, zn,… . Тогда формула Сл1(x, y) = (y0  `x0) Çi=1, w (yi
`x0) Çi=1, w (yi  xi Å Çj=0, i-1 xj) представляет двоичную функцию прибавления единицы. В этой формуле конъюнкция Çj=0, i-1 xi представляет перенос в i-й разряд, он равен 1 тогда и только тогда, когда все разряды от нулевого до (i - 1)-го единичные.
xi Å Çj=0, i-1 xj) представляет двоичную функцию прибавления единицы. В этой формуле конъюнкция Çj=0, i-1 xi представляет перенос в i-й разряд, он равен 1 тогда и только тогда, когда все разряды от нулевого до (i - 1)-го единичные.
Согласно преобразованиям из [1], формула
Сл1(x, u, y): (y0  `x0) (u0
`x0) (u0  x0) Çi=1,w (yi
x0) Çi=1,w (yi  xi Å ui) Çi=0,w (ui+1
xi Å ui) Çi=0,w (ui+1  ui xi)
ui xi)
д-эквивалентна первоначальной и также представляет функцию прибавления единицы. Легко увидеть, что новая переменная ui определяет перенос в i-ый разряд, который вычисляется после прибавления 1 к вектору с разрядами от нулевого до (i – 1)-го включительно. Перенос в нулевой разряд совпадает с нулевым разрядом самого числа.
Пример 1.2. Формула
Сл(x, у, z) = (z0 x0Åу0)(u1
x0Åу0)(u1 x0у0)Çi=1,w{(zi
x0у0)Çi=1,w{(zi xiÅуiÅui)(ui+1
xiÅуiÅui)(ui+1 ui(xiÚуi)Úxiуi)}
ui(xiÚуi)Úxiуi)}
представляет сложение x + у. Здесь x, y, z суть соответственно значения аргументов и суммы, а каждая переменная ui, i = 1, 2, … обозначает перенос в i–й разряд.
Пример 1.3. По аналогии с формулой Сл1(x, у) строится формула Выч1(x, у), представляющая разность у = x - 1:
Выч1(x, у) = Èi=0, wxiÉ {(y0  `x0) Çi=0,w(yi
`x0) Çi=0,w(yi  xiÅÇj=0, i-1xj)} {Çi=0,w`xi É Çi=0, w`yi}.
xiÅÇj=0, i-1xj)} {Çi=0,w`xi É Çi=0, w`yi}.
В этой формуле x, y соответственно значения аргументов и разности. При этом первый член конъюнкции является импликацией, посылка которой есть проверка условии, что аргумент не нулевой. В этом случае разность на 1 меньше аргумента. Заключение этой импликации представляет собой конъюнкцию. Первый ее член показывает, что нулевой компонент результата есть отрицание нулевого компонента аргумента. Второй - что занимаем мы из следующего разряда только в случае, когда рассматриваемый компонент аргумента равен нулю. Второй член формулы – также импликация, посылка которой истинна, если аргумент равен 0. Но тогда значение разности нулевое.
Избавившись от вложенности обобщенных связок, получим формулу Выч1(x, u, у) = Èi=0, wxiÉ{(y0 `x0)(u1
`x0)(u1 `x0)Çi=1, w (yi
`x0)Çi=1, w (yi xiÅui) Ù Ù (ui+1
xiÅui) Ù Ù (ui+1 ui`xi)} Ù {Çi=0, w`xi É Çi=0, w`yi}. Ее конъюнкция Çi=1, w(yi
ui`xi)} Ù {Çi=0, w`xi É Çi=0, w`yi}. Ее конъюнкция Çi=1, w(yi xiÅui)(ui+1
xiÅui)(ui+1 ui`xi) описывает вычисление компонентов разности и занимаемой в старшем разряде величины. Значение ui обозначает занимаемую величину в i+1-м разряде, в зависимости от наличия занимания в i-м разряде и значения i-го компонента аргумента.
ui`xi) описывает вычисление компонентов разности и занимаемой в старшем разряде величины. Значение ui обозначает занимаемую величину в i+1-м разряде, в зависимости от наличия занимания в i-м разряде и значения i-го компонента аргумента.
Пример 1.4. Аналогично представляются предикаты равенства и неравенства: x = y : Çi=0,w xi  yi; x > 0 : Èi=0,w xi.
yi; x > 0 : Èi=0,w xi.
Пример 1.5. Конъюнкция Çi=0,w xisi представляет двоичную константу s0, s1, s2, … .
Справедлива такая теорема.
Теорема 1.2. Пусть формулы F(x, y) и G(y, z) представляют двоичные функции соответственно y = f(x) и z = g(y). Тогда конъюнкция F(x, y)G(y, z) представляет суперпозицию z = f(g(y)).
Пример 1.6. Используя последнюю теорему о суперпозиции функций, приведем ряд формул, представляющих арифметические функции и отношения. Для начала построим формулу, представляющую функцию x + 2, суперпозицией двух функций прибавления единицы. Тогда формула, представляющая функцию прибавления 2, представляет собой конъюнкцию Сл1(x, y) Ù Сл1(y, z) = (y0  `x0) Çi=1, w(yi
`x0) Çi=1, w(yi  xi Å Çj=0, i-1 xj)(z0
xi Å Çj=0, i-1 xj)(z0  `y0) Çk=1, w(zk
`y0) Çk=1, w(zk  yk Å Çh=0, k-1 yh) º (y0
yk Å Çh=0, k-1 yh) º (y0  `x0)(z0
`x0)(z0  `y0)Çi=1, w(yi
`y0)Çi=1, w(yi  xi Å Çj=0, i-1 xj)Çk=1, w(zk
xi Å Çj=0, i-1 xj)Çk=1, w(zk  yk Å Çh=0, k-1 yh).
yk Å Çh=0, k-1 yh).
Преобразуя, получаем z0  x0. Используя две эквивалентности z1 º y1 Å y0, y1 º x1 Å x0, получаем z1 º x1 Å x0 Å`x0 º x1. Bспользуя две эквивалентности z2 º y2 Å y0y1, y2 º x2 Å x0x1, получаем z2 º x2 Å x0x1 Å`x0 (x1 Å x0) º x2 Å x0x1 Å`x0x1 º x2 Å x1. Используя две эквивалентности z3 º y3 Å y0y1y2, y3 º x3 Å x0x1x2, получаем z3 º x3 Å x0x1x2 Å`x0(x1 Å x0)(x2 Å x0x1) º x3 Å x1x2. Индукцией по k нетрудно доказать, что zk
x0. Используя две эквивалентности z1 º y1 Å y0, y1 º x1 Å x0, получаем z1 º x1 Å x0 Å`x0 º x1. Bспользуя две эквивалентности z2 º y2 Å y0y1, y2 º x2 Å x0x1, получаем z2 º x2 Å x0x1 Å`x0 (x1 Å x0) º x2 Å x0x1 Å`x0x1 º x2 Å x1. Используя две эквивалентности z3 º y3 Å y0y1y2, y3 º x3 Å x0x1x2, получаем z3 º x3 Å x0x1x2 Å`x0(x1 Å x0)(x2 Å x0x1) º x3 Å x1x2. Индукцией по k нетрудно доказать, что zk  xk Å Çh=1, k-1 xh , при k = 2, 3, … . Окончательная формула выглядит так: (y0
xk Å Çh=1, k-1 xh , при k = 2, 3, … . Окончательная формула выглядит так: (y0  x0)(y1
x0)(y1  `x1) Çi=2,w yi
`x1) Çi=2,w yi  xi Å Çj=1, i-1 xj. Формулы, представляющие функции: x + 3, x + 4, x + 5, x + 6 выглядят как соответственно: (y0 º`x0)(y1
xi Å Çj=1, i-1 xj. Формулы, представляющие функции: x + 3, x + 4, x + 5, x + 6 выглядят как соответственно: (y0 º`x0)(y1  x0 Å`x1) Çi=2,w(yi º xiÅx1Åx0`x1Çj=2, i-1 xj, (y0 º x0)(y1 º x1)(y2 º`x2) Çi=3,w yi º xi Å Çj=2, i-1 xj, (y0º`x0 )(y1 º x0 Å x1)(y2 º`x2 Å x0x1 ) Çi=3,w yi º xi Å(x2Å x0 x1`x2) Çj=3, i-1 xj, (y0º`x0)(y1
x0 Å`x1) Çi=2,w(yi º xiÅx1Åx0`x1Çj=2, i-1 xj, (y0 º x0)(y1 º x1)(y2 º`x2) Çi=3,w yi º xi Å Çj=2, i-1 xj, (y0º`x0 )(y1 º x0 Å x1)(y2 º`x2 Å x0x1 ) Çi=3,w yi º xi Å(x2Å x0 x1`x2) Çj=3, i-1 xj, (y0º`x0)(y1 `x1)(y2
`x1)(y2 x1Å`x2)(Çi=3,wyi
x1Å`x2)(Çi=3,wyi  xiÅ(x2 Å x1`x2)Çj=3, i-1 xj.
xiÅ(x2 Å x1`x2)Çj=3, i-1 xj.
Предикат y £ x представим формулой Çi=0,w(xi`yi É Èj=i+1,w`xjyj). Напомним, что в нашем представлении двоичных чисел старшие разряды располагаются правее. Функция z = x ¸ y представима формулой (x ≤ y É Çi=0,w`zi) Ù (x > y É (z0 x0Åy0) Ù u1º
x0Åy0) Ù u1º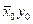 Ù Çi=1,w(zi
Ù Çi=1,w(zi xi Å yi Å ui) Ù (ui+1
xi Å yi Å ui) Ù (ui+1 `xiyi Ú ui(`xi Ú yi)) º (x ≤ y É Çi=0,w`zi) Ù (x > y É (z0
`xiyi Ú ui(`xi Ú yi)) º (x ≤ y É Çi=0,w`zi) Ù (x > y É (z0 x0Åy0) Ù u1º
x0Åy0) Ù u1º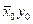 Ù Çi=1,w(zi
Ù Çi=1,w(zi xi Å yi Å ui) Ù (ui+1
xi Å yi Å ui) Ù (ui+1 `xiyi Ú ui(xi º yi)). Используя введенные соотношения, легко показать, что функция z = |x – y| вычисления абсолютного значения разности представима формулой: (x £ y É Выч(y, x, z))(y < x É Выч(x, y, z)).
`xiyi Ú ui(xi º yi)). Используя введенные соотношения, легко показать, что функция z = |x – y| вычисления абсолютного значения разности представима формулой: (x £ y É Выч(y, x, z))(y < x É Выч(x, y, z)).
Пример 1.7. Рассмотрим функцию y = SL(x) сдвига влево на один разряд бесконечного бинарного вектора. Эта функция представима формулой SLF(x, y) = 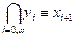 . В случае, когда мы рассматриваем конечные векторы, пусть длины h, то функция y = SLh(x) представима формулой SLFh(x, y) =
. В случае, когда мы рассматриваем конечные векторы, пусть длины h, то функция y = SLh(x) представима формулой SLFh(x, y) = 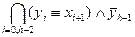 .
.
Справедлива следующая
Теорема 1.3. Функция y = cx двоичного умножения числа x на константу c представима примитивной формулой.
Просто доказывается такая
Теорема 1.4. Пусть арифметическая функция y = f(x1, x2, …, xn) представима примитивной формулой F(y, x1, x2, …, xn) и существует функция xi = f i-1(x1, …, xi-1, xi+1, …, xn, y). Тогда она также представима формулой F(y, x1, x2, …, xn).
Пример 1.8. Формула Сл1(x, y) = (y0  `x0)ÙÇi=1, w(yi
`x0)ÙÇi=1, w(yi  xiÅÇj=0, i-1 xj) представляет функцию прибавления единицы. Функция вычитания единицы (при условии, что вычитание происходит не из нулевого аргумента) представима формулой Выч1(x, у) = (y0
xiÅÇj=0, i-1 xj) представляет функцию прибавления единицы. Функция вычитания единицы (при условии, что вычитание происходит не из нулевого аргумента) представима формулой Выч1(x, у) = (y0  `x0) Ù Çi=0,w(yi
`x0) Ù Çi=0,w(yi  xiÅÇj=0, i-1`xj). После переименования переменных Выч1(x, у) превращается в формулу (y0
xiÅÇj=0, i-1`xj). После переименования переменных Выч1(x, у) превращается в формулу (y0  `x0) Ù Çi=0,w(xi
`x0) Ù Çi=0,w(xi  yiÅÇj=0, i-1`yj).
yiÅÇj=0, i-1`yj).
Из последней теоремы вытекает, что формула F(x, y, c) представляет функцию x = y/c целочисленного деления на константу c. Из этого следует такое утверждение.
Теорема 1.5. Функция нахождения целочисленного решения линейного уравнения с целыми коэффициентами представима примитивной формулой.
2. Представимость функций арифметики Пресбургера. Покажем, что все функции арифметики Пресбургера представимы примитивными формулами. Нам потребуется следующее определение программы.
Пусть X = {x1, x2, … } – входной, а Y = {y1, y2, …} – рабочий алфавиты. Буквы этих алфавитов назовем соответственно входными и рабочими переменными. Программа с такими входными и рабочими переменными - p(x1, x2, …, xn, y1, y2, …, ym) представляет собой ор-граф с вершинами трех типов: арифметические операторы 0(y) – присваивания переменной y нулевого значения, s(y) – прибавление к переменной y единицы, логический оператор u = v, где u, v – рабочие или входные переменные и единственная заключительная вершина. Каждая арифметическая вершина имеет ровно одного последователя, логическая – двух (один из которых называется 0-последователем, другой 1-последователем), а заключительная вершина последователей не имеет. Заключительная вершина помечена единственной рабочей переменной, которая называется выходной. Кроме того, одна из вершин программы является начальной.
Функцией, вычисляемой программой p, называется частичная функция fp такая, что fp(a1, a2, …, an) = b Û программа останавливается при значениях ее входных переменных x1 = a1, x2 = a2, …, xn = an и выходная переменная равна b.
Две программы эквивалентны, если они вычисляют одну функцию.
Существуют эквивалентные преобразования программ, которые позволяют получать программы с перечисленными ниже свойствами.
Свойство 1. Всякая программа эквивалентна такой, в которой в каждую арифметическую вершину ведет в точности одна дуга.
Поэтому ограничимся рассмотрением только таких программ, в которых несколько дуг могут вести только в логические вершины.
Свойство 2. Всякая программа в обычном базисе эквивалентна программе в расширенном логическом базисе: c = u, u + c1 = v + c2, где u, v – рабочие переменные, а c, c1, c2 – константы, в которой в каждую логическую вершину ведут несколько дуг или ей непосредственно предшествует логическая вершина.
Очевидно следующее утверждение.
Лемма 2.1. Пусть p есть программа, состоящая только из арифметических операторов. Тогда вычисляемая ею функция представляет собой прибавление константы, определяемой видом программы p.
Рассмотрим случай, когда программа содержит логические вершины, но не имеет циклов. В данном случае справедливо такое утверждение.
Теорема 2.2. Функция, вычисляемая программой без циклов в расширенном логическом базисе, представима примитивной формулой.
Справедлива такая
Лемма 2.3. Пусть p есть программа, представляющая собой единственный цикл, которому предшествует последовательность арифметических вершин, единственная логическая вершина имеет следующий вид: ее s-дуга принадлежит циклу, а (1-s)-дуга ведет в выходную вершину. Тогда программа p вычисляет функцию, представимую примитивной формулой.
На самом деле, программа с единственным циклом может содержать и несколько логических вершин, через которые этот цикл проходит. В этом случае аналогичное утверждение также верно. Чтобы не приводить громоздкого доказательства, покажем это для случая, когда цикл содержит только две логические вершины E(u, v): u + c1 = v + c2 и E(s, t): s + c3 = t + c4. По Свойству 2 они соседние, пусть s-дуга из E(u, v) ведет в E(s, t), l-дуга которой принадлежит циклу, а (1 - l)-дуга – не принадлежит.
Пусть в процессе однократного прохождения цикла переменные u, v, s, t получают приращение соответственно cu, cv, cs, ct. Для доказательства надо рассмотреть все значения пары (s, l): (0, 0), (0, 1), (1, 0), (1, 1).
1. Значение пары (s, l) есть (0, 0). В этом случае число прохождений цикла определяется как n = min(n1, n2), где n1 = 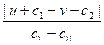 , n2 =
, n2 = 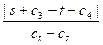 . Но все эти функции представимы примитивными формулами. В итоге всякая рабочая переменная цикла в результате вычисления увеличится на величину cn, где константа с определяется видом и расположением арифметических операторов цикла.
. Но все эти функции представимы примитивными формулами. В итоге всякая рабочая переменная цикла в результате вычисления увеличится на величину cn, где константа с определяется видом и расположением арифметических операторов цикла.
2. Значение пары (s, l) есть (0, 1). В этом случае число прохождений цикла определяется как n = min(n1, n2), где n1 = 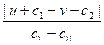 , а n2 определяет выполняется или не выполняется равенство s + c3 = t + c4 для начальных значений переменных s, t. В любом случае цикл проходится не более одного раза.
, а n2 определяет выполняется или не выполняется равенство s + c3 = t + c4 для начальных значений переменных s, t. В любом случае цикл проходится не более одного раза.
3. Аналогично разбираются оставшиеся два случая. В этом случае цикл также проходит не более одного раза, а вычисляемая программой функция представима примитивной формулой.
Рассмотрим арифметические программы над полным базисом, арифметические операторы которого суть 0(x) – обнуление переменной x, s(x) – прибавление единицы, и единственный логический E(x, y) – равенство переменных. В [5] показано, что всякая функция арифметики Пресбургера вычисляется такой арифметической программой над полным базисом без вложенных циклов. Отсюда следует, что если заменить в программе без вложенных циклов каждый цикл на функцию, представляющую собой прибавление константы, то в таком расширенном базисе программа представляет собой ор-дерево, в котором уже три типа арифметических вершин, а каждая бинарная вершина - логическая. Назовем такие программы расширенными.
Справедливо такое утверждение.
Теорема 2.4. Функция, вычисляемая расширенной программой, представима примитивной формулой.
В результате получаем
Следствие. Всякая функция арифметики Пресбургера представима примитивной формулой.
 science-review.ru
science-review.ru