Scientific journal

Scientific Review. Physics and Mathematics

Введение. Исходя из важности проблемы установления сложности вычислений для прикладных задач [1, 2, 3], в статье предлагается универсальный формализм, позволяющий анализировать вычисления из достаточно широкого класса. Он представляется как расширение пропозиционального языка за счет бесконечных логических связок, позволяющее представлять все вычислимые функции [4, 5]. Однако, при вполне естественных ограничениях удается выделить так называемый примитивный пропозициональный язык, в котором представимы только функции арифметики Пресбургера. Эти ограничения касаются окрестности вхождений переменных, если формулы рассматривать как бесконечные последовательности символов. В результате все такие формулы характеризуются бинарными программами с ограниченной шириной. В статье рассматриваются некоторые свойства примитивных пропозициональных формул. В последующем будет проиллюстрировано их использование для исследования задач вычислительной сложности.

1. Обобщенные пропозициональные формулы. Далее рассматривается расширение пропозиционального языка над базисом {Ú, Ù, Ø} путем обобщений дизъюнкции и конъюнкции на не более, чем счетное множество аргументов. Для обобщенных дизъюнкции и конъюнкции будем использовать выражения соответственно Èi=k, h и Çi=k, h, где i называется индексом этой связки, k – нижней границей, а h – верхней. k и h – это либо константы, либо символ бесконечности w, либо целочисленные функции, зависящие от других индексов.

Введем определение формулы в расширенном базисе. Для обозначения формул будем употреблять буквы f, g, h, … с индексами.

1. Полагаем, что задано счетное множество переменных x, y, z, … , возможно с индексами, каждая из которых есть формула. Одна переменная может обладать несколькими индексами.

2. Если A, A1 – формулы, то A Ú A1, A Ù A1 и`A суть формулы.

3. Если h, k – нижняя и верхняя границы, fi, i = k, k+1, k+2, …, h – суть формулы, то Èi=k, h fi и Çi=k, h fi также суть формулы. Будем говорить, что все формулы fi находятся в области действия связок соответственно Èi=k, h и Çi=k, h. Это же относится к каждой их подформуле. Если fi содержит в качестве подформулы обобщенную формулу, то ее границы могут быть либо константами, либо символом бесконечности, либо значением некоторой целочисленной функции от i и других индексов (эти функции назовем граничными).

Пример 1.1. Следующие выражения суть формулы: Èi=0, w xi, Çi=0,w yi+5, Èi=0,w Çj=0, i yj+2, Èi=0, w Çj=2i, 3i yi, j, Èi=0, w Çj=0, w xi,j Ú yj+1.

Что касается семантики обобщенных формул, то укажем несколько.

1) Временная семантика с дискретным временем.

2) Семантика линейного порядка с определенными ограничениями, которые задаются обобщенными формулами.

3) Семантика в виде вычислимых функций, когда все одноимённые переменные с различными индексами, например, x0, x1, x2, … трактуются как компоненты бинарного вектора x0x1x2 … , представляющего двоичную запись числа.

Наиболее важная для нас семантика обобщенных формул связана с представлением вычислимых функций, когда формула является характеристической для функции. В частности, обобщенная формула F(x1, x2, …, xn, y) представляет двоичную функцию y = f(x1, x2, …, xn), если при означивании переменных x1, x2, …, xn, y соответственно бинарными векторами s1, s2, …, sn, sn+1 формула F(s1, s2, …, sn, sn+1) истинна тогда и только тогда, когда f(s1, s2, …, sn) = sn+1.

2. Свойства обобщенных формул. Как обычно, назовем дизъюнктом (конъюнктом) конечную или бесконечную дизъюнкцию (конъюнкцию) литер. Если в формуле А встречается подформула В, то обозначим это через А(В). Множество всех переменных произвольной формулы F обозначим Var(F).

Логические значения функций в расширенном базисе вычисляются путем обобщения таблиц истинности бинарных связок: обобщенная дизъюнкция Èi=k, h fi истинна тогда и только тогда, когда истинен, по меньшей мере, один ее член fi, i Î {k, k+1, k+2, …, h}, а обобщенная конъюнкция Çi=k, h fi тогда и только тогда, когда истинны все ее члены fi, i = k, k+1, k+2, …, h.

Две формулы F и G логически эквивалентны (обозначается F G), если множества их единичных означиваний совпадают. Поэтому формула Èi=0, w fi (Çi=0, w fi) эквивалентна такой, которая получается из нее любой перестановкой дизъюнктивных (конъюнктивных) членов fi и исключением одной из двух логически эквивалентных формул fi и fj при i 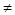j.

Бесконечные связки позволяют ввести обобщения различных логических эквивалентностей. Рассмотрим следующий пример.

Пример 2.1. 1. Известно, что если импликация A É B тождественно истинная, то верна эквивалентность A Ù B º A. Одно из ее обобщений на случай бесконечных формул выглядит следующим образом. Пусть в формуле A = Èi=0,wÇj=0,i fj, конъюнкция Çi=0,wf0Éfi тождественно истинная. Тогда справедлива эквивалентность A º f0.

2. В булевой алгебре формулы (x1 º y1 Ù x2 º y2) É (x1 Ú x2 º y1Ú y2) и (x1 º y1 Ù x2 º y2) É (x1Ùx2 º y1Ù y2) тождественно истинные. Обобщение их на случай бесконечных связок являются формулы соответственно Çi=0,w(xi º yi) É (È i=0,wxi º Èi=0,wyi) и Çi=0,w(xi º yi) É (Ç i=0,wxi º Çi=0,wyi), которые также тождественно истинные.

3. Для обобщенных формул легко привести эквивалентности, которых нет в булевой логике. Например, Çi=0,wÇj=0,w fi,j º Ç j=0,wÇi=0,w fi,j, È i=0,wÈ j=0,w fi,j º Èj=0,wÈ i=0,w fi,j. Здесь fi,j – логические формулы. То, что они с индексами, в данном случае никак не влияет на вид переменных, из которых они построены.

4. Перестановка подформу в обобщенных дизъюнкции и конъюнкции, в общем случае, не сохраняет эквивалентность. Имеется большое число различных комбинаций обобщенных связок, которые не перестановочны. Например, в формуле Çi=0,wÇj=0,i fi,j обобщенные связки не перестановочны, т.к. внутренняя зависит от внешней.

5. Используя введенные обобщенные связки, можно конструировать другие обобщенные связки. Например, обобщенная эквивалентность выглядит так ºi=0,w xi и выражается следующим образом: Çi=0,w xi Ú Çi=0,w`xi. Она принимает значение истина тогда и только тогда, когда все переменные xi, i = 0, 1, … имеют одинаковые логические значения.

6. Обобщенные формулы могут выступать в роли характеристических функций. Функция z = åi=0,w xi есть сложение по модулю два для бесконечных двоичных последовательностей. Ее характеристическая функция такая: (y0 º x0) Ù Çi=1, w (yi º yi - 1 Å xi) Ù (Èi=0,w Çj=i,w yj º z).

Просто доказывается следующая лемма.

Лемма 2.1. Верны следующие эквивалентности:

1. ØÈ i=k, h fi 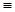Ç i=k, h`fi ; ØÇ i=k, h fi 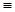È i=k, h`fi ; Ø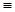`F F.

2. Если формула A не содержит переменных, индексы которых зависят от i, то справедливы эквивалентности: A Ú Ç i=k, h fi 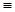Ç i=k, h (A Ú fi) и A Ù È i=k, h fi 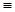È i=k, h (A Ù fi).

3. Если формула А(G) получается из А(F) заменой формулы F на G, и F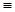G, то справедлива эквивалентность А(F)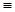А(G).

4. Çi= k, h (fi Ù gi) º Çi= k, h fi Ù Çi= k, h gi; Èi= k, h (fi Ú gi) º (Èi= k, h fi) Ú (Èi= k, h gi).

Из эквивалентностей п.4 легко получить такое утверждение.

Следствие. Каждая обобщенная формула эквивалентна обобщенной формуле, у которой в подформуле Çi=k,h fi, в которой нет вложенных обобщенных связок, все формулы fi суть дизъюнкты, а в подформуле Èi=k,h fi, в которой также нет вложенных обобщенных связок, все формулы fi – конъюнкты.

Пусть G = Èi=k, h fi(xh(i)) (G = Çi=k, h fi(xh(i))) есть формула, и xh(i) – переменная, индекс которой определяется целочисленной функцией h, существенно зависящей от аргумента i. Тогда говорим, что переменная xh(i) управляется связкой Èi=k, h (Çi=k, h). Если индекс переменной не является функцией от i, то она не управляется связкой Èi=k, h (Çi=k, h). Заметим, что переменная может находиться в области действия обобщенной связки, но не управляться ею.

Пример 2.2. В формуле Èi=0, w xi+1 + y1 = zi - i+1 переменная xi+1 управляется связкой Èi=0, w, а переменные y1 и zi - i+1 – нет.

Введем аналогичные понятия для обобщенных связок. Пусть G = Èi=k, h fi(Нi) (G = Çi=k, h fi(Нi)) есть формула, и Нi имеет вид Èj=s, p Nj (или Ç j=s, p Nj), причем границы s или p – функции от i. Тогда говорим, что Нi управляется связкой Èi=k, h (Çi=k, h). Если обе границы s и p не зависят от i, то Èj=s, p Nj (или Ç j=s, p Nj) не управляется связкой Èi=k, h (Çi=k, h). Как и в случае переменных, обобщенная подформула может находиться в области действия обобщенной связки, но не управляться ею.

Пример 2.3. В формуле Èi=0, w(Ç j=i+1, w xj+1) Ú Ç k=1, w yk подформула Ç j=i+1, w xj+1 управляется связкой Èi=0, w , а Ç k=1, w yk – не управляется.

Для дальнейшего нам потребуется ввести так называемую приведенную форму обобщенных формул, которая характеризуется тем, что в области действия обобщенных связок находятся лишь управляемые ими переменные. Подформула называется свободной от индекса i, если индексы ее переменных и верхние и нижние границы ее обобщенных связок не зависят от i.

Справедлива такая лемма.

Лемма 2.2. Пусть формула G имеет вид Çi=k, h fi(X) (Èi=k, h fi(X)), где X – подформула свободная от индекса i. Тогда формула G эквивалентно преобразуется в формулу, у которой подформула X не управляется обобщенной связкой Çi=k, h (Èi=k, h).

Пример 2.4. Пусть А есть формула Çi=0,w (xi Çj=0,w (xi+5 Ú yj)). Применив к ней эквивалентности из Леммы 1.1, получим следующие эквивалентные формулы: Çi=0,w xi Ù Çi=0,w Çj=0,w (xi+5 Ú yj); Çi=0,w xi Ù Çi=0,w (xi+5 Ú Çj=0,w yj); Çi=0,w xi Ù (Çj=0,w yj Ú Çi=0,w xi+5); (Çi=0,w xi Ù Çj=0,w yj) Ú (Çi=0,w xi Ù Çi=0,w xi+5); (Çi=0,w xi Ù Çj=0,w yj) Ú (Çi=0,w xi xi+5);

Таким образом, A эквивалентна формуле, в которой каждая обобщенная связка управляет только теми переменными, индексы которых зависят от индекса управляющей связки.

Из последней леммы получаем

Следствие. Всякая обобщенная формула эквивалентна формуле, в которой,

во-первых, всякая обобщенная связка с постоянными границами (в том числе w) не управляется никакими другими обобщенными связками;

во-вторых, каждая обобщенная связка с индексом i управляет лишь переменными и обобщенными связками, индексы которых зависят от i;

наконец, отрицания располагаются непосредственно над переменными. (Такие формулы назовем приведенными).

В дальнейшем мы ограничимся рассмотрением только приведенных формул.

Понятно, что если на вид индексов переменных, а также вид граничных функций у обобщенных связок не накладывать никаких ограничений, то получается очень богатый язык, первоначальное исследование которого затруднительно. Поэтому введем ряд ограничений, которые позволят сузить язык до приемлемого размера, одновременно сохраняя ряд его интересных свойств. Но прежде введем такое определение: целочисленная функция от одного аргумента называется сдвиговой, если она есть функция прибавления константы.

Полагаем, что рассматриваемые формулы образованы из счетного множества xi, yi, zi, …, i = 0, 1, … переменных. Переменные xi (yi, zi и т.д.) назовем однотипными, соответственно x-переменными (y-переменными, z-переменными и т.д.), x (y, z и т.д.) является типом переменных xi (yi, zi и т.д.). Тип произвольной переменной x обозначим Type(x). Если Var есть множество переменных, то Varx будет его подмножество всех x-переменных. Аналогично вводятся подмножества y-переменных, z-переменных и т.д. соответственно Vary, Varz, и т.д.

Если Var есть множество переменных, то типом – Type(Var) этого множества назовем совокупность их типов. Если F есть формула, то Type(Var(F)) называется ее типом и обозначается Type(F).

Введем понятие длины обобщенной формулы F. Длиной обобщенной формулы называется число вхождений всех ее переменных.

Пример 2.5. Длина формулы (y0 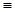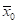)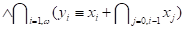равна 5.

Назовем обобщенный пропозициональный язык примитивным, если его формулы удовлетворяют следующим ограничениям.

1. Каждая формула обладает типом ограниченной мощности и конечной длиной.

2. Каждая переменная, характеризуется не более, чем одним индексом, который есть либо константа, либо значение сдвиговой функции от индекса связки, управляющей этой переменной.

3. Каждая обобщенная связка имеет граничными значениями либо константу, либо символ бесконечности, либо значение сдвиговой функции от индекса обобщенной связки, в области действия которой она находится.

Пример 2.6. Следующие формулы не принадлежат примитивному языку:

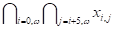(переменные характеризуются двумя индексами),

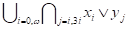(граничная функция у одной из обобщенных связок не сдвиговые).

Следующие формулы примитивные:

, .

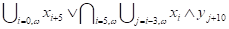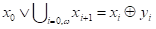Далее, если не оговорено противное, будем рассматривать лишь примитивные формулы.

3. Семантика примитивных формул. Приведем несколько семантик введенного языка. Это представляет интерес, так как обобщенные связки существенно расширяют выразительные возможности булевского языка.

1. Первую семантику назовем временной, так как она наглядно представляется в виде выполнения событий в дискретном времени. Для этого будем ассоциировать с каждым типом переменных (для наглядности, пусть x-переменных) некоторое событие, которое может наступать и не наступать в указанные моменты времени. Тогда истинность переменной xi трактуется как наступление этого события в i-й момент времени, ложность – не наступление. Время принимается дискретным, однонаправленным: 0, 1, 2, … – суть моменты времени.

Пример 3.1. При такой семантике конъюнкция Çi = 0,wxi обозначает наступление события x в каждый момент времени; формула x0 Ù Çi = 0,w(xi Å xi+1) – наступление события x в точности в четные моменты времени; формула Çi = 0,w(xi É xi+1) обозначает, что если для некоторого момента наступило событие x, то оно наступает и во все последующие моменты; Çi=0,w(xi É Èj=i+1,wxj) обозначает, что если событие x наступает в некоторый момент времени, то оно повторяется бесконечное число раз впоследствии; Èi=0,w(`xi Çj=0,i-1yj) обозначает, что имеется некоторый момент времени в который событие x не наступает, а событие y наступает во все момент времени до этого.

Пример 3.2. Используя временную семантику, можно описывать, например, технологические переходы, как это делается в сетевом планировании. Для этого покажем, как построить аналог утверждения: событие z наступает только после наступления событий x и y. Это сводится к конъюнкции следующих высказываний:

Çi = 0,w(xi É xi+1), Çi = 0,w(yi É yi+1) – однократное наступление события влечет его наступление во все последующие момент времени;

Çi=0,w(xi É Èk=i+1,wzk) – событие z наступает после наступления события x;

Çi=0,w(yi É Èk=i+1,wzk) – событие z наступает после наступления события y;

Çi=0,w(`xi É Çk=0,i`zk) – если событие x не наступает, то не наступает событие z;

Çi=0,w(`yi É Çk=0,i`zk) – если событие y не наступает, то не наступает событие z.

Используя временную семантику примитивных формул, можно решать задачи составления технологических цепочек с целью нахождения требуемой последовательности выполнения работ.

2. Вторая семантика задается формулами первого порядка над линейно упорядоченным множеством, на котором определены отношения порядка (<) и равенства (=). При этом обобщенная конъюнкция и дизъюнкция трактуются как кванторы соответственно общности и существования с ограничениями. Предикатная сигнатура состоит из счетного множества сингулярных предикатов, каждому типу переменных (для определенности пусть x-типу) соответствует свой предикат (в данном случае X(x)). Индексам соответствуют индивидные переменные, которые являются аргументами предикатов.

Далее нам потребуются т.н. ограниченные кванторы, которые представляют собой обычные кванторы с ограничениями на вид связываемых ими переменных. При этом в формулировке ограничений участвуют сдвиговые функции. Так $x(x < y+5) трактуется, как существование такого x, что выполняется неравенство x < y+5, "x(x ³y) – для всякого x, который не меньше y. Каждый ограниченный квантор имеет единственное условие, относящееся к связываемой им переменной.

Нетрудно видеть, как обобщенные формулы переводятся на описанный язык первого порядка. С другой стороны, всякая формула первого порядка с ограниченными кванторами, в которой отношения порядка не встречаются нигде, кроме ограниченных кванторов переводится на язык примитивных формул. Такой перевод имеет смысл, так как позволяет доказывать разрешимость классов формул первого порядка.

Пример 3.2. Примитивная формула Çi=0,w(xi É Èk=i+1,wzk) переводится в формулу первого порядка – "x(X(x) É $z(z > x)Z(z)).

3. Наконец, еще одна семантика примитивных формул основывается на представлении каждого типа переменных как бесконечного двоичного вектора. Тогда, например, все x-переменные x0, x1, x2, … трактуются как компоненты бинарного вектора x0x1x2 … . Такой бинарный вектор можно интерпретировать как совокупность двоичных чисел, младшие разряды которых располагаются левее, и для всякого конечного двоичного числа имеется ограниченный отрезок с единичным правым разрядом, правее которого располагается бесконечный нулевой вектор.

Пример 3.3. 101100 … 000 … = 1310, 1111100…000… = 3110.

Бесконечный вектор, у которого правее всякого разряда имеется единичный разряд, не имеет интерпретации в виде конечных чисел, такой вектор представляет собой бесконечное двоичное число и есть интерпретация формулы Çi=0,w(xi É Èj=i+1,wxj).

Интерпретацией формулы Çi=0,w(xi É Èj=i+1,wÇk=j,w`xk) являются все конечные двоичные числа. Действительно, конъюнкция Çk=j,w`xk понимается здесь как бесконечный вектор, у которого, начиная с j-го компонента, располагаются только нули. Тогда дизъюнкция Èj=i+1,wÇk=j,w`xk интерпретируется как существование такого вектора, бесконечная последовательность которого начинается с некоторого разряда, расположенного правее (i+1)-го разряда. Но тогда, если имеется i-й единичный разряд, то правее существует бесконечная нулевая последовательность, начинающаяся с (i+1)-го разряда.

Подводя итог, скажем, что выразительные возможности примитивного языка достаточно широкие, чтобы получать результаты, которые переносятся на смежные области: модальные логики, исчисления первого порядка и вычислимые функции.

4. Эквивалентные преобразования обощенных формул. Обобщенные формулы эквивалентно приводимы к некоторому достаточно простому виду, который позволяет судить об их выразительных возможностях. Чтобы показать это, сформулируем ряд вспомогательных утверждений.

Лемма 4.1. Пусть формула А = (u0 f0) Ù Çi = 0,w(ui+1 ui Ù fi+1), где u0, u1, u2, … - переменные и f0, f1, f2, … - формулы, не содержащие переменных u0, u1, u2, …. Тогда имеют место эквивалентность А º Çi = 0,w (ui Çj=0, i fj).

Следствие. Справедлива эквивалентность

((u0 f0) Ù Çi=0,w (ui+1 ui Ù fi+1)) Çi=0,w (ui Çj=0, i fj).

Аналогичное утверждение верно для дизъюнкции.

Лемма 4.2. Пусть формула А = (u0 f0) Ù Çi = 0,w(ui+1 ui Ú fi+1)}, где u0, u1, u2, … – переменные и f0, f1, f2, … - формулы, не содержащие переменных u0, u1, u2, …. Тогда имеет место эквивалентность А º Çi = 0,w(ui Èj=0, i fj).

Следствие. Справедлива эквивалентность

((u0f0)ÙÇi=0,w(ui+1uiÚfi+1))Çi=0,w(uiºÈj=0, ifj).

Рассмотрим случай, когда обобщенные связки имеют изменяемую нижнюю границу. В этом случае ситуация несколько отличается от рассмотренной. Это демонстрируют следующие утверждения.

Лемма 4.3. Пусть формула А = Çi=0,w (ui ui+1 Ù fi) Ù (Èi=0, w ui Èi=0, w Çj=i,w fj), где u0, u1, u2, … – переменные и f0, f1, f2, … - формулы, не содержащие переменных u0, u1, u2, …. Тогда имеет место эквивалентность А º Çi=0,w (ui Çj= i, w fj).

Следствие. Справедлива эквивалентность

Çi=0,w(ui ui+1Ùfi) Ù (Èi=0, w uiÈi=0, wÇj=i,w fj) º Çi=0,w(uiÇj= i, w fj).

Аналогичные утверждения имеют место, когда рассматривается обобщенная дизъюнкция.

Лемма 4.4. Пусть формула А = Çi=0,w(ui ui+1 Ú fi) Ù (Çi=0, w ui Çi=0, w Èj=i, w fj), где u0, u1, u2, … – переменные и f0, f1, f2, … - формулы, не содержащие переменных u0, u1, u2, …. Тогда имеет место эквивалентность А º Çi=0,w(ui Èj= i, w fj).

Лемма 4.5. Для всякого h ³ 0 справедлива эквивалентность Çi=0, w Èj=i,w fj º Çi=h, w Èj=i,w fj.

Следствие. Для всякого h ³ 0 справедлива эквивалентность

Çi=0,w(ui ui+1 Ú fi) Ù (Çi=0, w ui Çi=h, w Èj=i,w fj) º Çi=0,w (ui Èj= i, w fj).

Лемма 4.6. Для всякого h ³ 0 справедлива эквивалентность Èi=0, wÇj=i,w fj º Èi=h, wÇj=i,w fj.

Следствие. Для всякого h ³ 0 справедлива эквивалентность

Çi=0,w(ui ui+1 Ú fi) Ù (Èi=0, w ui Èi=h, w Çj=i,w fj) º Çi=0,w (ui Ç j= i, w fj).

Назовем формулы

(u0 f0) Ù Çi=0,w (ui+1 ui Ù fi+1), (u0 f0) Ù Çi=0,w (ui+1 ui Ú fi+1),

Çi=0,w(ui ui+1 Ù fi) Ù (Èi=0, w ui Èi=h, w Çj=0,w fj),

Çi=0,w(ui ui+1 Ú fi) Ù (Çi=0, w ui Çi=h, w Èj=i,w fj), h ³ 0,

рекурсивными определениями переменных ui, i = 0, 1, … . Доказанные эквивалентности позволят, во-первых, определить вид формул, представляющих собой конъюнкцию рекурсивных определений и примитивной формулы, в которой отсутствуют вложенные обобщенные связки, и во-вторых, доказать, что каждая примитивная формула, в определенном смысле, эквивалентна формуле указанного вида.

5. Достаточная эквивалентность. В этом разделе введем отношение эквивалентности обощенных формул – так называемую достаточную эквивалентность. С этой целью покажем, что формулы F(G) и (u G) Ù F(u), в определенном смысле, эквивалентны. Здесь F(G) есть формула, содержащая подформулу G, и u - новая переменная, не входящая в Var(F(G)).

Очевидны следующие два утверждения.

Лемма 5.1. Пусть при некотором означивании переменных Var(F(G)) значение функции F(G) есть l, а функции G ? s; l, s Î{0, 1}. Тогда при том же означивании переменных Var(F(G)) и при значении u равном s значение функции (u G) Ù F(u) также равно l.

Лемма 5.2. Пусть при некотором означивании переменных {u} È Var(F(G)) значение функции (u G) Ù F(u) есть истина. Тогда при том же означивании переменных Var(F(G)) значение F(G) также есть истина.

Таким образом, если функция F(G) истинна в точности при означиваниях: s1, s2, …, sm … переменных Var(F(G)), и при этих означиваниях функция G принимает значения соответственно l1, l2, …, lm, … , то функция (u G) Ù F(u) истинна в точности при таких означиваниях l1s1, l2s2, …, l msm, … переменных {u} È Var(F(G)). Как видно, проекции единичных означиваний обеих функций F(G) и (u G) Ù F(u) на переменные Var(F(G)) совпадают.

Пусть F и Н суть логические функции, V = Var(F) Ç Var(H). Тогда эти функции называются достаточно эквивалентными (д-эквивалентными) относительно переменных множества V, если множества проекций единичных означиваний обеих функций на переменные V совпадают.

Из последних двух утверждений вытекают такие следствия.

Следствие 1. Функции F(G) и (u G) Ù F(u) д-эквивалентны относительно переменных Var(F(G)).

Следствие 2. Примитивная формула F(Èi=h,k fi), в которой выделенная обобщенная связка не содержит управляемых обобщенных связок, д-эквивалентна формуле (u Èi=h,k fi) Ù F(u), где u – новая переменная.

Следствие 3. Примитивная формула F(Çi=h,k fi), в которой выделенная обобщенная связка не содержит управляемых обобщенных связок, д-эквивалентна формуле (u Çi=h,k fi) Ù F(u), где u – новая переменная.

Введем следующее определение. Пусть в примитивной формуле имеется подформула Çi=h,k fi, в которой границы не являются функциями от индексов других обобщенных связок. Тогда связка Çi=h,k называется независимой от других.

Следствие 4. Всякая примитивная формула д-эквивалентна примитивной формуле, в которой отсутствует вложенность независимых обобщенных связок.

Теперь необходимо рассмотреть случай, когда обобщенные связки управляются другими обобщенными связками. С этой целью докажем утверждение.

Теорема 5.3. Примитивная формула F(Çj=0,i fj), в которой подформула Çj=0, i fj не содержит вложенных обобщенных связок, д-эквивалентна относительно переменных Var(F) формуле F* = (u0 f0) Ù Çi =0,w(ui+1 ui Ù fi+1) Ù F(ui), где переменные u0, u1, u2, … не встречаются в F.

Аналогично доказывается такая теорема.

Теорема 5.4. Примитивная формула F(Èj=0, i fj), в которой подформула Èj=0, i fj не имеет вложенных обобщенных связок, д-эквивалентна относительно переменных Var(F) формуле F* = (u0 f0) Ù Èi =0,w (ui+1 ui Ùfi+1) Ù F(ui), где u0, u1, u2, … - переменные, не встречающиеся в F.

Таким образом, если формула содержит обобщенную связку без вложенных обобщенных связок, верхняя граница которой определяется индексом управляющей связки, то она преобразуется в д-эквивалентную, в которой вместо этой подформулы располагается новая переменная, а сама подформула элиминирована путем введения рекурсивного определения.

Рассмотрим теперь случаи, когда нижняя граница обобщенной связки определяется индексом другой управляющей связки.

Докажем следующее утверждение.

Теорема 5.5. Примитивная формула F(Çj=i,w fj), в которой подформула Çj=i,w fj не имеет вложенных обобщенных связок, д-эквивалентна относительно переменных Var(F) формуле F* = (Çi =0,w ui ui+1 Ùfi) Ù (Èi=0, w ui Èi=0, w Çj=i, w fj) Ù F(ui), где u0, u1, u2, … - переменные, не встречающиеся в F.

Аналогично доказывается такая теорема.

Теорема 5.6. Примитивная формула F(Èj=i,w fj), в которой подформула Èj=i,w fj не имеет вложенных обобщенных связок, д-эквивалентна относительно переменных Var(F) формуле F* = (Èi =0,w ui+1 ui Ú fi+1) Ù (Çi=0, w ui Çi=0, w Èj=0, i fj) Ù F(ui), где u0, u1, u2, … - переменные, не встречающиеся в F.

Последние два случая отличаются от двух предыдущих, что вызвано зависимостью нижней границы от индекса управляющей связки. Отличие, в первую очередь, состоит в том, что вместе с рекурсивным определением появляется еще ограничение на значения новых переменных. Содержательно оно формулируется так: все переменные ui, i = 0, 1, … истинные, если среди функций fi, i = 0, 1, …, присутствует хотя бы одна истинная.

Из последних четырех утверждений получаем утверждение о нормальной д-эквивалентной форме обобщенных формул.

Теорема 5.7. Всякая примитивная формула д-эквивалентно представима в виде конъюнкции F0 Ù F1, где F0 – это конъюнкция рекурсивных определений, в которой вложенность обобщенных связок не превосходит двух, и F1 – это примитивная формула, не имеющая вложенных обобщенных формул. (Назовем такое д-эквивалентное представление д-эквивалентной формой (д.э.ф.) исходной формулы).

Пример 5.1. Применим описанные преобразования к формуле

(y0 `x0) Ù Çi=1,w (yi xi Å Çj=0, i-1 xj),

где Å - сложение по модулю два.

По Теореме 5.3 эта формула д-эквивалентна следующей

(u0 x0) Ù Çi=0,w (ui+1 ui Ù xi+1) Ù (y0 `x0) Ù Çi=1,w(yi xi Å ui-1)

Вложенность обобщенных связок в последней формуле отсутствует.

Пример 5.2. Применим описанные преобразования к формуле

R(х, у) = (x0a0x1a1 … xkak) Ù (y0b0y1b1 … yhbh) Ù (Çj=1,w xk+j yh+j) Ù

Ú Èm=1,w (Çi=0,m-1(xi1-a0Ú xi+11-a1 Ú … Ú xi+k1-ak)) Ù (xma0xm+1a1 … xm+kak) Ù

(Çj=0,m-1 xj yj) Ù (ymb0ym+1b1 … ym+hbh) Ù (Çj=m+1,w xk+j yh+j),

где верхние индексы принадлежат множеству {0, 1}, и экспоненциальная функция понимается, как принято в булевой алгебре. Для определенности полагаем, что k £ h.

Введем следующие сокращения. Обозначим подформулу xi1-a0Ú xi+11-a1 Ú … Ú xi+k1-akчерез`ai; xma0xm+1a1 … xm+kakчерез am; ymb0ym+1b1 … ym+hbhчерез bm; Çj=0,m xj º yj через [x y]m; конъюнкцию Çj=m,w xk+j º yh+j через [x y]m. Согласно теоремам 5.3 и 5.5 эта формула д-эквивалентна формуле

R*(х, у, u, v, w) = a0 Ù b0 Ù [x y]0 Ú u0 `a0 Ù Çi=0,w (ui+1 ui Ù`ai+1) Ù v0 (x0 y0) Ù

Çi=0,w (vi+1 vi Ù xi+1 yi+1) Ù Çi=0,w (wiwi+1Ù xk+i+1 yh+i+1) Ù

(Èi=0,w wi Èi=0,w Çj=0, i (xk+j yh+j)) Ù Èm=1,w (um-1 Ù am Ù bm Ù vm Ù wm).

Вложенность обобщенных связок в этой формуле отсутствует за исключением члена Èi=0,w wi Èi=0,w Çj=0, i (xk+j yh+j) рекурсивного определения.