science-review.ru
Введение. Классическая теория ЭМП базируется на фундаментальных уравнениях – уравнениях Максвелла, которые используются также и для построения квантовой теории ЭМП. Непрерывные характеристики поля: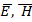 
– напряженностей электрической и магнитной составляющих; 
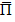– вектора Пойнтинга; 
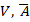– скалярного электрического и векторного магнитного потенциалов несут в себе непосредственный физический смысл и обуславливают образность классической теории.
Однако между классической и квантовой теориями господствует парадигма разделения сфер применения каждой теории. Условием демаркации областей правомерности каждой теории выступает длина электромагнитной волны.
Глубоко продвинутая для физического описания микромира квантовая теория сильно формализована и математизирована. Её корректным и точным вычислительным результатам не хватает образности квантовых процессов. В частности, квантовая теория не смогла установить внутреннюю структуру фотона и его пространственную локализацию. С другой стороны не раскрыт физический механизм квантово-волнового дуализма, также отсутствует понимание электрического заряда [1] и т.п. Для преодоления трудностей современной квантовой теории необходимы разработки классической теории.
В работе [2] предложена модель электромагнитного процесса на основе нового подхода решения волнового уравнения электромагнитного поля, возбуждаемого орбитальным электроном в центральном поле. При этом волновое уравнение при кулоновской калибровке для векторного потенциала усреднялось за время периода орбитального вращения электрона, что приводило к взаимной компенсации электронного тока и тока смещения кулоновского поля. Поэтому волновое уравнение становится однородным:
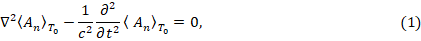
где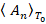 
– усредненная за период T0 вращения электрона проекция векторного потенциала на нормаль к неподвижной полуплоскости, перпендикулярной к плоскости орбиты.
В такой постановке однородное ДУ (1) описывает стационарный свободный процесс с собственной частотой колебания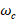 
, которая физически связана с частотой 
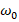вращения электрона 
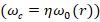. Решение ДУ (1) определялось в комплексной форме
Для стационарного процесса при t = 0 волновое уравнение (1) для комплексной амплитуды векторного потенциала становится уравнением Гельмгольца
которое в центрально-симметричном поле допускает решение, подобное решению стационарного уравнения Шредингера для атома водорода [3]:
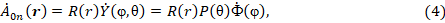
где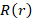 
– радиальная функция, 
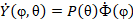– сферическая функция, 
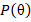– присоединенные функции Лежандра.
Комплексная функция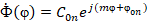 
с постоянной интегрирования 
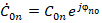есть комплексная форма общего решения дифференциального уравнения.
где с учетом требования однозначности функции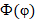 
значение 
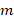должно быть целым натуральным числом (
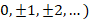и получил называние магнитного квантового числа [3].
Выражение (4) с учетом (2) в сферической системе координат примет вид:
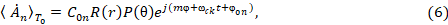
где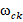 
– квантованные значения частот колебаний векторного потенциала.
Таким образом, выражение (5) описывает вращающую полевую структуру векторного потенциала – стационарную замкнутую волну. Угловая скорость вращения замкнутой волны вокруг оси z равна: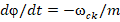 
.
Цель исследования. Математическое моделирование и исследование вектора Пойнтинга и связанных с ним орбитальных моментов вращающего ЭМП.
Восстановление составляющих векторного потенциала. В декартовой системе координат вектор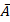 
и его проекция на единичный направляющий вектор 
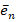примут соответствующий вид:
,
,
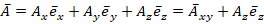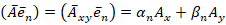где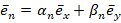 
– нормальный вектор к фиксированной неподвижной плоскости 
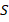, проходящей через ось Oz. С учетом (4) представим выражение (2):
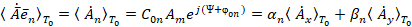. (7)
Подставляя (7) (аналогично как в [2] при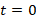 
) в уравнение (1), получим при фиксированном, но произвольном векторе 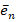два независимых уравнения Гельмгольца
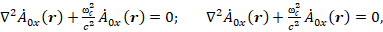(8)
для которых решения по форме совпадают с выражением (5):
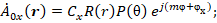
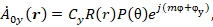(9)
где 
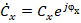и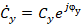 
постоянные интегрирования.
Для согласования постоянных интегрирования в выражениях (9) представим (5) в виде двух систем ДУ первых порядков:
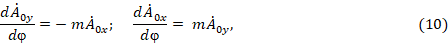
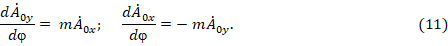
Системе (10) соответствуют условия: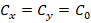 
, 
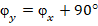, а системе (11) –
, 
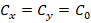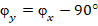. (12)
Угловая скорость вращения замкнутой волны вокруг оси z отрицательная (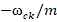
), то вращение направлено в противоположную сторону координате 
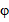(по часовой стрелке, см. рис. в [2]). Поэтому выбираем условия (12), а выражения (9) примут вид:
=
; 
=
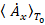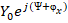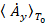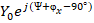, (13)
в которых использованы следующие обозначения:
; 
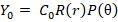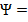
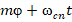. (14)
Вращающий параллельно плоскости орбиты векторный потенциал в комплексной форме с учетом (13) примет следующий вид:
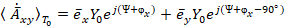. (15)
Применяя к (15) классическую формулу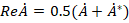 
, запишем вращающий векторный потенциал в вещественной форме:
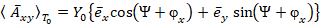. (16)
Неизвестную проекцию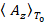 
векторного потенциала на ось 
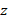на основе выражения (16) свяжем с вектора 
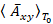по уравнению кулоновской калибровки:
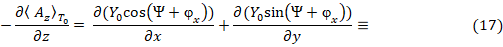
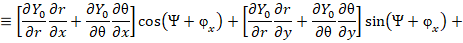
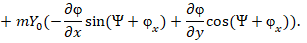
Подставляя в (17) для сферической системы координат следующие соотношения
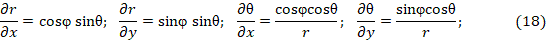
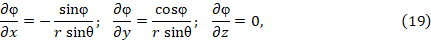
получим искомую связь в сферических координатах:
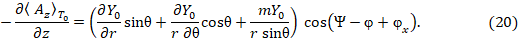
Заметим, что кулоновская калибровка правомерна для вещественной составляющей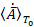 
.
Записав кулоновскую калибровку через комплексные значения векторного потенциала по типовой формуле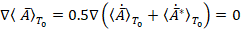 
[4], получим:
С учетом зависимости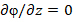 
в соответствии с (6) понятна структура производной по переменной 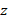от проекции 
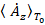векторного потенциала в комплексной форме:
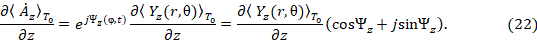
Из сопоставления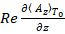 
в (22) и (20), получим:
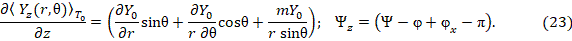
Далее определим дивергенцию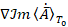 
из выражений (15), (22) – (23):
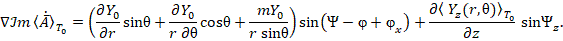
Подставив (23) в последнее выражение и учтя (21), получим:
Утверждение 1. Для комплексного и комплексно-сопряженного векторного потенциала структуры (6) правомерна кулоновская калибровка.
Взяв производную по времени от составляющей векторного потенциала (16), получим выражение напряженности электрического поля:
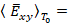
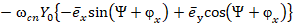. (25)
Вектор Пойнтинга. Выразим вектор Пойнтинга через векторный потенциал ЭМП [5]. Выразив в комплексно-сопряженной форме полный векторный потенциал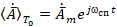 
, 
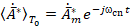, будем иметь:
, 
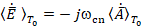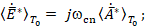
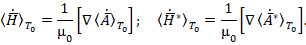
Учитывая кулоновскую калибровку (24), определим выражения:
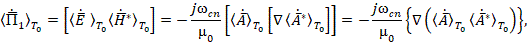
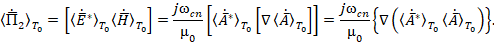
Значение постоянной составляющей вектора Пойнтинга орбитального электромагнитного поля определим по типовой формуле [6]:
.
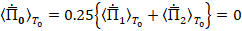Утверждение 2. Отсутствует излучение энергии орбитального ЭМП.
Магнитная индукция поля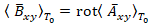
в декартовой системе координат будет:
=
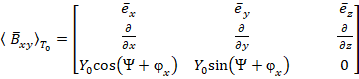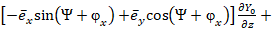
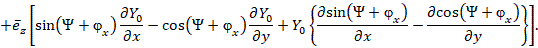
Учтя выражения (18) – (19), получим магнитную индукцию:
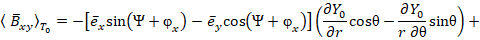
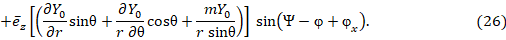
Используя силовые характеристики поля (25) – (26), получим вектор Пойнтинга вращающей составляющей ЭМП:
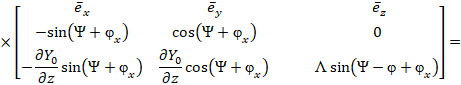
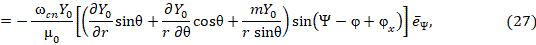
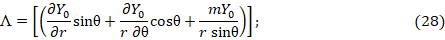
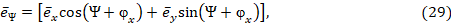
Постоянная составляющая вектора Пойнтинга вращательной составляющей поля (16):
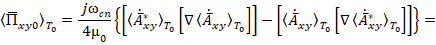
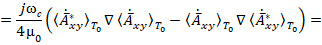
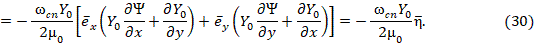
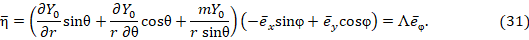
где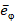 
– азимутальный орт сферической и цилиндрической систем координат.
Таким образом, доказано, векторные линии постоянной составляющей вектора Пойнтинга совпадают с азимутальными координатными линиями, поэтому они замкнуты, и они охватывают ось z.
Проекция момента количества движения на ось z. Воспользуемся механическими свойствами электромагнитного поля, характеристиками которых являются вектор плотности импульса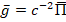 
и плотность момента импульса 
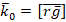[5]. Вычислим момент количества движения 
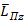вращающейся электромагнитной полевой структуры, подставляя в типовую формулу выражение (27):
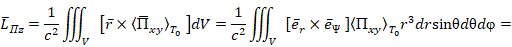
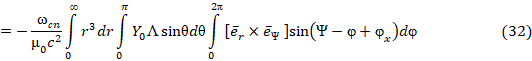
и результат векторного произведения единичных направляющих векторов
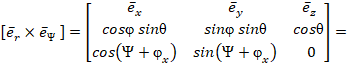
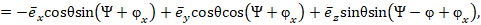
и учитывая ненулевой интеграл по азимутальной переменной 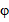на интервале 
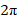от гармонических тригонометрических функций, получим:
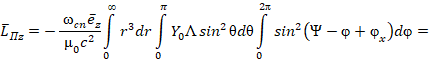
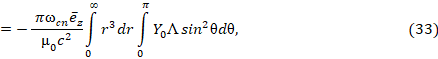
который разобьем на слагаемые, при этом обозначив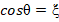 
, 
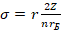, где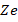 
- заряд ядра:
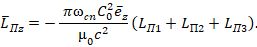
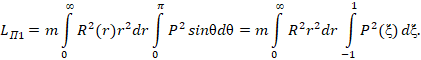
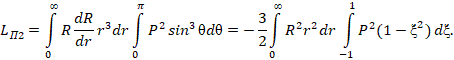
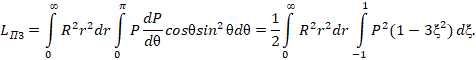
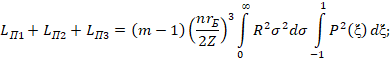
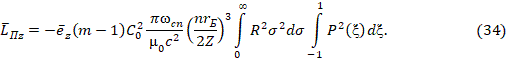
Таким образом, установлено, что вращающая составляющая ЭМП (замкнутая волна), создающая поток электромагнитной мощности, циркулирующей вокруг оси z, обладает квантованным моментом количества движения. Назовем его электромагнитным.
Результирующий орбитальный момент количества движения (вдоль оси вращения – оси z) состоит из электромагнитного момента и момента количества движения частицы (электрона), равный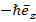 
. Знак минус указывает на то, что вектор Пойнтинга (27), (30) вращающей составляющей ЭМП совпадает с направлением орбитального вращения электрона (взятого по часовой стрелке). При этом результирующий орбитальный момент количества движения должен соответствовать научно-обоснованному значению 
:
.
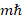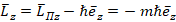Требование выполнения этого условия приводит к следующей нормировке постоянной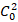 
:
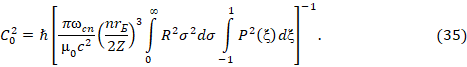
В рассматриваемой модели в формировании квантовых свойств принимают участие классический электрон и новый элемент – электромагнитная вращающая полевая структура (замкнутая волна). Каждому элементу соответствует согласованное число степеней свободы квантовых свойств – полевой структуре соответствует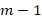 
значений, а частице соответствует единичное значение, что указывает на корректность предлагаемой теории.
Магнитный момент. В классической теории и в квантовой механике орбитальный момент количества движения и магнитный момент связаны гиромагнитным отношением. Однако причиной магнитного момента в классике это электронный ток, а в квантовой механике это особый ток – плотность тока вероятности.
В работе [7] утверждается, что вектор Пойнтинга можно выразить через произведение приложенного напряжения к системе (или к её участку) на вектор плотности эквивалентного тока, совпадающего по направлению с вектором Пойнтинга. Поэтому, если имеется поток электромагнитной мощности, задаваемый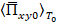 
, с ненулевой постоянной составляющей, то он может быть источником локализации постоянной составляющей плотности эквивалентного тока:
где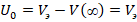 
напряжение на поверхности микросистемы, равный некоторому эквивалентному потенциалу 
.
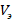Ток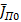 
неизвестной физической природы создает магнитный момент, который вычислим по методике, излагаемой в учебной литературе по квантовой механике.
Через элемент площади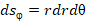 
, нормальный азимутальной координатной линии j протекает элемент тока 
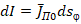, создающий элемент магнитного момента 
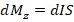, где площадь элемента тока 
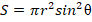. Подставив (30) в (36), получим элемент проекции магнитного момента 
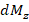через элемент поверхности 
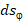и результирующую проекцию магнитного момента 
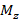на ось 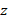соответственно:
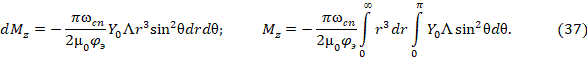
Направление орбитального магнитного момента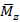 
связано с направлением тока правилом правого винта, а направление тока, согласно (36), определяется направлением вектора Пойнтинга 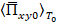, поэтому 
.
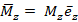Подчиняя моменты (37) и (33) гиромагнитному отношению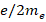 
(
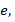
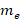– заряд и масса покоя электрона соответственно), то получим
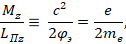
из которого следует известное выражение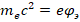 
, вытекающее из предположения, что масса покоя электрона обусловлена массой создаваемого им электростатического поля. При этом 
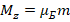, где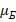 
– магнетон Бора.
Таким образом, в выражении (36) в качестве разности потенциалов электромагнитной системы, состоящей из орбитального электрона и вращающего ЭМП, выступает электростатический потенциал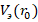 
, создаваемый точечным зарядом электрона на расстоянии классического радиуса электрона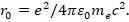 
Заключение.
Продолжена реализация, начатая в [2], математических моделей квантовых свойств орбитального электрона в центрально симметричном поле в рамках классической теории на основе нового подхода решения волнового уравнения.
1. Если в работе [2] обоснована причина отсутствия излучения энергии орбитальным электроном, то в настоящей работе проведено обоснование отсутствия излучения энергии орбитального электромагнитного поля.
2. В рамках классической теории построена корректная модель квантованных проекций на ось z орбитального момента количества движения и магнитного момента орбитального электрона, которые совпали с научно обоснованными результатами. Этот фактор может свидетельствовать о правомерности развиваемого подхода изучения квантовых свойств микромира.
3. Подведена физическая основа орбитальным квантованным моментам. В частности, в формирование моментов вносят вклад как вращающееся электромагнитное поле (со степенью свободы m-1, где m –магнитное квантовое число), так и орбитальное движение электрона (со степенью свободы 1), которые в сумме дают туже степень свободы (m), что и квантовая теория. А корректная согласованность результатов моделирования научно-обоснованному результату дают надежду на перспективность рассматриваемого метода изучения квантовых явлений с целью преодоления трудностей современной теории, отмеченных во введении.
4. Подтверждено научное положение, выдвинутое в работе [7], что вектор Пойнтинга потока электромагнитной мощности является причиной локализации дополнительного тока, а источником этого тока выступает электрический потенциал на «поверхности» электрона. Так в работе [7] в рамках классической теории это положение применено для преодоления противоречия между электромагнитной массой и инерционной массой электрона, то в этой работе оно подводит физическую причину для утверждения орбитального квантованного магнитного момента.