ВВЕДЕНИЕ
В последние годы искусственные нейронные сети уже достигли производительности, близкой или превосходящей производительность людей в некоторых областях. Одним из преимуществ этого технологического прорыва является упрощение сравнения различных нейронных сетей и производительности человека, чтобы углубить наше понимание человеческого познания. В последние годы область нейронных сетей претерпела существенную революцию, чему способствовали подходы к глубокому обучению [1]. Различные архитектуры достигли производительности, подобной человеческой, в областях, которые ранее считались исключительной прерогативой человеческого мозга, таких как восприятие [2] или язык [3]. Частично этот успех проистекает из идей, предоставленных когнитивными науками, в которых решения, основанные на мозге, реализуются в функциональных моделях [4]. И наоборот, можно исследовать вычислительные процессы, происходящие в человеческом мозге, сравнивая их с искусственными функциональными моделями.
Теоретически нейронная сеть с прямой подачей (FNN) может аппроксимировать любую функцию с произвольной точностью, поэтому нет необходимости в рекуррентной нейронной сети (RNN) [5]. Однако, это не означает, что FNN можно использовать в любых проектах, связанных с последовательными данными. Известно, что FNN можно передавать свои временные ряды в сети прямой связи, имея входной слой, содержащий входные данные из предыдущих временных точек, таким образом, эффективно преобразуя проблему временных рядов в проблему прямой трансляции. Однако, при этом нужно будет заранее выбрать длину ввода, и так как нельзя будет изучать функции, зависящие от входных данных, происходивших. Все это можно решить, имея RNN, который теоретически может хранить информацию сколь угодно давние в его контекстном слое. Однако на практике возникнет проблема с градиентным взрывом / исчезновением.
RNN использует метод корректировки весов нейронной сети на основе частоты ошибок, зарегистрированных в предыдущую эпоху. Правильно отрегулировав веса, можно снизить частоту ошибок и повысить надежность модели за счет расширения ее применимости. Градиент функции потерь для одного веса вычисляется алгоритмом обратного распространения нейронной сети с использованием правила цепочки. В отличие от встроенного прямого вычисления, он эффективно вычисляет по одному слою за раз. RNN может обрабатывать входные последовательности разной длины, используя их внутреннее состояние, которое может представлять форму памяти. Поэтому их можно использовать для таких приложений, как распознавание речи или рукописного ввода.
МАТЕРИАЛЫ И МЕТОДЫ
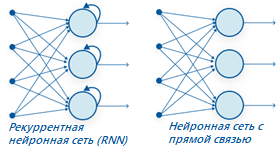
Нейронная сеть с прямой подачей (FNN или CNN)- это искусственная нейронная сеть, в которой нет обратной связи от выхода к входу. Можно также рассматривать его как сеть без циклического соединения между узлами (Рис.1). В архитектуре FNN существуют три уровня (входной, скрытый и выходной) и поток информации идет только в прямом направлении. Обратного потока нет, и, следовательно, название «нейронная сеть с прямой подачей» оправдано. Рекуррентные нейронные сети (RNN) представляют собой современный метод последовательной обработки данных. Это первый алгоритм с внутренней памятью, который запоминает входные данные, что делает его идеальным для задач, связанных с последовательными данными в машинном обучении (рис.2). Подход глубокого обучения для моделирования последовательных данных- это рекуррентные нейронные сети (RNN). Для модели с глубокой обратной связью могут потребоваться конкретные параметры для каждого элемента последовательности.
|
|
|
|
Рис.1. Схема FNN |
Рис.2. Схема RNN |
Рекуррентные нейронные сети используют одинаковые веса для каждого элемента последовательности, уменьшая количество параметров и позволяя модели обобщаться на последовательности различной длины. Из-за своего алгоритма RNN могут работать только со структурированными данными, отличных от последовательных, таких как географические или графические данные. Рекуррентные нейронные сети, как и многие другие методы глубокого обучения, являются относительно старыми. Впервые они были разработаны в 1980-х годах, однако их потенциал не оценили до сих пор. Появление долговременной кратковременной памяти (LSTM) в 1990-х годах в сочетании с увеличением вычислительной мощности и огромными объемами данных, с которыми нам сейчас приходится иметь дело, действительно выдвинуло RNN на передний план. Нейронные сети имитируют функции человеческого мозга в области искусственного интеллекта, машинного обучения и глубокого обучения, позволяя компьютерным программам распознавать шаблоны и решать общие проблемы. RNN- это тип нейронной сети, который может использоваться для моделирования данных в последовательностях. Рекуррентные нейронные сети, которые формируются из сетей прямой связи, по своей архитектуре и поведению отдаленно похожей на человеческий мозг. Проще говоря, рекуррентные нейронные сети могут предвосхищать последовательные данные так, как этого не могут другие алгоритмы.
Все входные и выходные данные в стандартных нейронных сетях независимы друг от друга, однако в некоторых случаях, например, при прогнозировании следующего слова фразы, необходимы предыдущие слова, и поэтому предыдущие слова необходимо запоминать. В результате был создан RNN, который использовал скрытый слой для преодоления этой проблемы. Наиболее важным компонентом RNN является скрытое состояние, которое запоминает конкретную информацию о последовательности. RNN имеют память, в которой хранится вся информация о вычислениях и эта сеть использует одинаковые настройки для каждого ввода, поскольку дает одинаковый результат, выполняя одну и ту же задачу для всех входных данных или скрытых слоев.
Рекуррентная нейронная сеть (RNN) и прямая нейронная сеть (FNN)
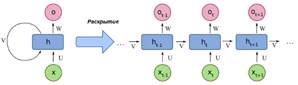
Нейронная сеть с прямой связью имеет только один маршрут потока информации: от входного слоя к выходному слою, проходя через скрытые слои. Данные передаются по сети по прямому маршруту, никогда не проходя через один и тот же узел дважды. Информационный поток между RNN и FNN показан на рисунке 3. Нейронные сети с прямой связью плохо предсказывают, что произойдет дальше, потому что у них нет памяти о полученной информации.
|
|
|
|
Рис.3. Информационный поток между RNN и FNN |
|
Поскольку она просто анализирует текущие входные данные, сеть с прямой связью не имеет представления о временном порядке. Помимо обучения, она не помнит, что происходило в прошлом этого процесса. Информация находится в цикле RNN через цикл. Прежде чем выносить суждение, он оценивает текущие входные данные, а также то, что он узнал из прошлых входных данных. С другой стороны, рекуррентная нейронная сеть может вспоминать из свой внутренней памяти, создавая выходные данные, копируя их, а затем возвращая в сеть.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ОБСУЖДЕНИЕ
Реализация нейронной сети с прямой связью в Python
Этап создания выборочных весов. Веса используются для описания мощности нейронной связи. Он варьируется от 0 до 1.
Определение архитектуры нейронной сети, включающая три узла с весами:
c1 = num.zeros((1,inputlayer_dimensionality)) # смещение для слоя 1
c2 = num.zeros((1, hiddenlayer_dimensionality)) # смещение для слоя 2
c3 = num.zeros((1,outputlayer_dimensionality)) # смещение для слоя 3
Для каждого узла были даны другие измерения. Измерения будут использоваться позже для вычисления взвешенной суммы нейронов (сумма весов, входного сигнала и элемента смещения). Все веса, предоставленные в первом, втором и третьем слоях, используются для вычисления взвешенной суммы нейронов в первом, втором и третьем скрытых слоях. На последнем уровне, как обычно, применяется функция softmax.
d1 = X.dot(a1) + c1 # первый скрытый слой
q1 = num.tanh(z1)
d2 = q1.dot(a2) + c2 # второй скрытый слой
q2 = num.tanh(z2)
d3 = q2.dot(a3) + c3 # третий скрытый слой
probs = num.exp(d3) / num.sum(num.exp(d3), axis=1, keepdims=True)
Список чисел, отправляемых этой функции, преобразуется в список вероятностей, вероятности которых пропорциональны числам в списке. Чтобы достичь выходного уровня, распространение будет происходить по нескольким слоям, которые включают первый, второй и третий скрытые слои. Функция активации определяет как взвешенная сумма преобразуется в выходные данные с каждого уровня сети. Ниже показаны особенности сети с прямым распространением активации:
· FNN вычисляется на основе tanh функции до 6 нейронов в 1-м слое
· FNN с 1-го уровня вычисляется на основе tanh функции до 6 нейронов во 2-м слое.
· FNN со 2-го уровня вычисляется на основе tanh функции до 3 нейронов в 3-м слое.
· Вероятность вычисляется как результат с использованием функции softmax.
Реализация нейронной сети с рекуррентной нейронной сетью
Какими бы сильными не были рекуррентные нейронные сети, однако они уязвимы для проблем обучения, связанных с градиентом. Рассмотрим две проблемы стандартных RNN.
Есть две ключевые проблемы, которые пришлось преодолеть RNN, но для того, чтобы понять их, нужно сначала понять, что такое градиент. Что касается его входных данных, градиент является частной производной и градиент определяет, насколько сильно изменяется результат функции при незначительном изменении входных данных. Наклон функции также известен как ее градиент. Чем круче наклон, тем быстрее модель может обучаться, тем выше градиент. С другой стороны, модель прекратит обучение, если наклон равен нулю. Градиент используется для измерения изменения всех весов по отношению к изменению ошибки.
· Взрывающиеся (exploding) градиенты: взрывающиеся градиенты возникают, когда алгоритм присваивает весам абсурдно высокий приоритет без видимой причины. К счастью, усечение или уменьшение градиентов является простым решением этой проблемы (рис.4).
· Исчезающие (vanishing) градиенты: исчезающие градиенты возникают, когда значения градиента слишком малы, что приводит к остановке обучения модели или занимает слишком много времени (рис.4). Это была большая проблема в 1990-х годах, и ее было гораздо сложнее решить, чем взрывающиеся градиенты. Однако, есть способы решения этой проблемы:
Ограничить количество градиентов при обучении модели, чтобы предотвратить их взрыв. Это называется градиентным отсечением [6].
Предотвратить уменьшение весов до нуля, установив их начальные значения в единичные матрицы и ноль для их смещений, где инициализация веса - технический термин для процедуры.
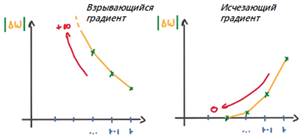
Рис.4. График градиентов
Для теста использовался набор последовательных данных о солнечных пятнах, которые относятся к периоду с 1749 по 2013 год и представляют собой среднемесячные значения для каждого месяца [7]. Создаем модель, которая включает в себя слои SimpleRNN и Dense для изучения последовательных данных банковского учреждения [8]. Функция create_RNN используется для вычисления политики управления.
def create_RNN(hidd_units, dense_units, input_shape, activation
FNNModel = Sequential()
FNNModel.add(SimpleRNN(hidd_units,input_shape=input_shape,activation=activation[0]))
FNNModel.add(Dense(units=dense_units, activation=activation[1]))
FNNModel.compile(loss='mean_squared_error', optimizer='adam')# модели и метрики
return FNNModel
Где FNNModel.add(SimpleRNN)- полностью связная RNN, где выход предыдущего временного интервала должен быть подан на следующий временной интервал. FNNModel.add(Dense)- обычный слой нейронной сети с глубокой связью.
Используем функцию create_RNN в качестве конструктора для создания модели RNN:
TestModel = create_RNN(2, 1, (3,1), activation=['linear', 'linear'])
x1 = test_FNNModel.get_weights()[0], a1 = test_FNNModel.get_weights()[2], x3 = test_FNNModel.get_weights()[3], a2 = test_FNNModel.get_weights()[4]
Выходная матрица:
x1 = [[0,10637812 1,14110394]] x2 = [[-0,32743179 0,94560836] [ 0,94487935 0. 0,32817713]] a1 = [0. 0.] x3 = [[-0,55914178] [-0,55291787]] a2 = [0.]
Слой SimpleRNN создал два скрытых объекта, в то время как плотный слой создает один плотный объект и все они возвращаются в объект тестовые модели. Оба слоя используют линейную функцию активации с 3х1 входным значением формы. В данном анализе был использован метод рандомизированного взвешивания, при этом важным компонентом является выяснение того, как элементы работают вместе для создания конечного результата.
|
|
|
|
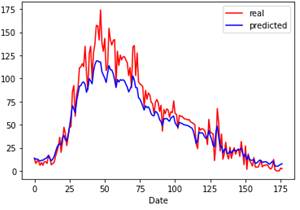
Рис. 5. Прогноз на 5 дней |
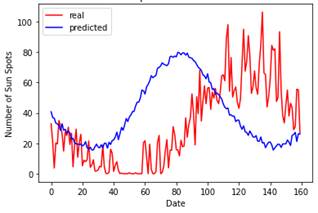
Рис. 6. Прогноз на 60 дней |
При прогнозе на 5 дней картина предсказаний достаточно радостная, нет выпадения цикла и пики вполне симметричны, далее стоит проверить, сможет ли модель RNN предсказать один полный 11- летний цикл. Для нашего набора данных каждая точка данных представляет один месяц, и понятно, что следует ожидать цикла солнечных пятен каждые 11 лет, поэтому прогноз был на 132 точки данных в будущем времени. Однако, чтобы захватить часть следующего цикла, необходимо использовать где- то 160 дней для предсказания вперед по временной шкале. Таким образом, был применен период в 360 дней: назад 200 дней и вперед 160 дней. Модель RNN правильно фиксирует сезонность или циклический компонент временного ряда, однако график смещается, а пик и впадина не совпадают (рис.6).
Таким образом, при реализации были выявлены следующие различия сетей FNN и RNN: В отличии от сетей прямой связи, рекуррентные нейронные сети имеют один весовой параметр на всех уровнях сети. Обучение с подкреплением все еще может быть достигнуто путем корректировки этих весов с использованием обратного распространения и градиентного спуска. Рекуррентные нейронные сети содержат цикл обратной связи, который позволяет возвращать данные обратно на вход, прежде чем они будут снова отправлены для дальнейшей обработки и окончательного вывода. В то время как нейронные сети с прямой связью просто пересылают данные с ввода на вывод. В нейронных сетях с прямой связью данные могут поступать только в одном направлении. Данные с предыдущих уровней не могут быть сохранены из-за этого шаблона перемещения вперед; следовательно, нет внутреннего состояния или памяти. RNN, с другой стороны, использует цикл для перебора данных, позволяя ему отслеживать как старую, так и новую информацию.
ЗАКЛЮЧЕНИЕ
При использовании рекуррентных нейронных сетей надо учитывать, что– это универсальный инструмент, который можно использовать в самых разных ситуациях и различными наборами временных рядов [9]. Важно, что RNN может обрабатывать входные данные любой длины, при этом модель RNN моделируется так, чтобы запоминать каждую информацию в течение всего времени и даже если размер входных данных становится больше, размер модели не увеличивается, что очень полезно при любом прогнозе во временных рядах. Однако у рекуррентных нейронных сетей есть один недостаток. У них возникают проблемы с изучением долгосрочных зависимостей, что означает, что они не понимают взаимосвязи между данными, разделенными несколькими шагами. Например, при предвосхищении прогноза пятен может потребоваться больше контекста. Это известно как проблема исчезающего градиента, и она решается с использованием особого типа рекуррентных нейронных сетей, называемых сетями долговременной кратковременной памяти (LSTM). Используя модели RNN и наборы временных рядов, можно решать большой ряд проблем, в том числе: распознавание объектов, генерацию музыки, автопереводы, анализ и прогноз болезней и т.д.
Библиографическая ссылка
Эвиев В.А., Маштыков С.С., Маштыков Д.С., Мацаков Б.В., Джахнаева Е.Н. ПРОБЛЕМЫ ПРОГНОЗИРОВАНИЯ В НАБОРАХ ВРЕМЕННЫХ РЯДОВ С ПОМОЩЬЮ РЕКУРРЕНТНЫХ НЕЙРОННЫХ СЕТЕЙ // Научное обозрение. Физико-математические науки . 2022. № 1. ;URL: https://physics-mathematics.ru/ru/article/view?id=103 (дата обращения: 04.03.2026).
 science-review.ru
science-review.ru