Введение. В энергетике [1], на транспорте, при перекачке природного газа и в других крупных отраслях народного хозяйства большое распространение получили газотурбинные установки или двигатели (ГТУ или ГТД), отличающиеся компактностью, возможностью использования широкого ассортимента газообразных и жидких топлив, быстротой набора и сброса мощности, относительно высоким КПД и прочими достоинствами [2].
Абсолютное большинство современных ГТУ разрабатываются и работают по так называемому циклу Брайтона, в котором подвод теплоты к рабочему телу осуществляется в камере сгорания при постоянном давлении. На рис. 1 изображены идеальный и реальный циклы ГТУ, построенные в координатах T-s (температура-энтропия).
В идеальном цикле Брайтона последовательно (и, естественно, повторно) по отношению к рабочему телу протекают следующие термодинамические процессы:
1-2 изоэнтропное (при постоянной энтропии) сжатие в компрессоре, на привод которого затрачивается работа;
2-3 изобарный (при постоянном давлении) подвод теплоты в камере сгорания;
3-4 изоэнтропное расширение в турбине с совершением полезной работы;
4-1 изобарный отвод теплоты (сброс продуктов сгорания в окружающую среду).
Так как реальные процессы подвода и отвода теплоты осуществляются в адиабатных (без теплообмена с окружающей средой), а не в изоэнтропных процессах, то реальный цикл Брайтона изображается линиями 1-2p-3-4p-1 на рис. 1.
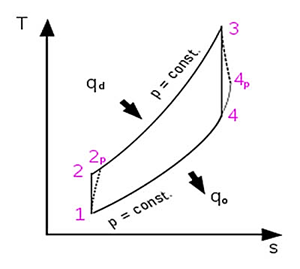
Рис.1. T-s диаграмма идеального и реального циклов Брайтона.
qd – это теплота, вводимая в цикл рабочим телом при его горении в камере сгорания, q0 – теплота, сбрасываемая с выхлопными газами в атмосферу.
Цель исследования. Для оценки эффективности цикла, изображённого на рис. 1, необходимо вычислить ряд его параметров (давления и температуры в характерных точках, степень повышения давления в компрессоре, КПД, полезную работу). Формулы для определения этих характеристик широко представлены в классической литературе по теплофизике, например, в [3, 4].
Однако, для повышения качества проектирования газотурбинных установок, работающих по циклу Брайтона, необходимо создать способ быстрого нахождения характерных точек данного цикла [4], а главное его оптимальных параметров, обеспечивающих наиболее эффективное преобразование теплоты, выделяемой при сгорании топлива, в работу, совершаемую турбиной. В связи с этим, целью данной работы является разработка компьютерной программы, автоматизирующей нахождение необходимых зависимостей и построение характеристик цикла Брайтона [5].
Материал и методы исследования. Основным параметром, характеризующим оптимальность идеального цикла Брайтона, является так называемая работа цикла, то есть разность работы расширения рабочего тела в турбине и его сжатия в компрессоре. Для реального же цикла показателем, характеризующим его эффективность, является внутренний КПД, равный отношению работы цикла к теплоте, подведённой к рабочему телу в камере сгорания при нагреве его от температуры T2 (на выходе из компрессора) до температуры T3 (на входе в турбину) [6].
Указанные параметры эффективности цикла зависят в первую очередь от степени повышения давления в компрессоре πк, поэтому основной задачей разрабатываемой программы является построение графических зависимостей от этого параметра работы идеального цикла и КПД реального цикла. Также программа должна автоматически находить и указывать на графиках оптимальные точки.
Для создания расчётной программы использовался алгоритм определения положения точек начала и окончания термодинамических процессов ПТУ, а также показателей термодинамической эффективности установки, приведённый в работе [5].
Для написания кода программы был выбран наиболее современный язык программирования Python, характеризующийся следующими достоинствами:
- бесплатность и широкое распространение, большое количество публикаций по его использованию в сети интернет;
- приспособленность к созданию программ для выполнения разнообразных задач (универсальность);
- широкие возможности для разработки качественного и удобного графического интерфейса;
- возможность подключения огромного количества библиотек и модулей для выполнения специфических задач, в свою очередь созданных на языке Python.
Для проектирования интерфейса пользователя программы была использована специальная библиотека Tkinter. Команды данного модуля позволили в главном окне программы разместить все необходимые надписи, поля ввода исходных данных, виртуальные кнопки, запускающие расчёты идеального и реального циклов [7].
Для отображения результатов расчёта и оптимизации в графическом виде использована библиотека Matplotlib для Python [8].
Полученный таким образом интерфейс программы с введёнными исходными данными для расчёта примера показан на рис. 2.
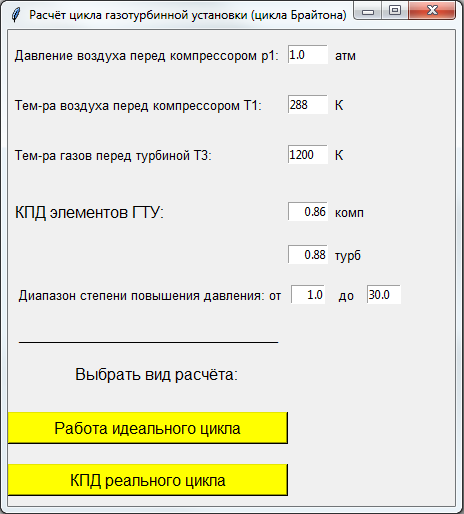
Рис. 2. Интерфейс программы расчёта идеального и реального циклов Брайтона.
В качестве исходных данных используются давление и температура воздуха перед компрессором (как правило, атмосферные), температура газов перед турбиной, а также КПД компрессора и турбины. Для проведения оптимизационных расчётов и построения графиков также необходимо задать диапазон изменения степени повышения давления в компрессоре. Значения в полях ввода можно редактировать, производя расчёты цикла с любыми значениями указанных параметров.
Результаты. Приведённые на рис. 2 исходные данные были использованы для расчёта примера, описанного в книге [3] и демонстрации возможностей созданной программы.
Результаты расчёта главного оптимизируемого параметра идеального цикла Брайтона – его работы в зависимости от степени повышения давления в компрессоре πк приведены на рис. 3.
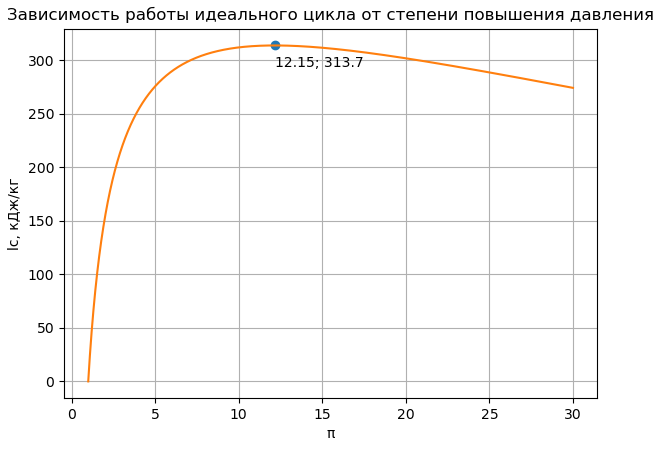
Рис. 3. Зависимость работы идеального цикла Брайтона от степени повышения давления в компрессоре.
На график автоматически выводятся координаты точки, в которой достигается наибольшая работа исследуемого цикла. Для выбора максимального значения из всех рассчитанных значений работы при разных πк использована ещё одна библиотека - Numpy для языка Python, предназначенная для работы с таблицами и массивами данных, организованных различным образом. В данном случае по индексу расположения в массиве максимального значения работы найден соответствующий индекс значения степени повышения давления.
В рассчитанном примере максимально достижимая работа цикла составляет 313,7 кДж/кг при πк =12,15. Отсюда можно сделать вывод, что компрессор в данном случае при его дальнейшем детальном проектировании необходимо рассчитывать именно на такую степень повышения давления.
Подобный график можно получить для любого набора исходных данных. Например, при повышении температуры перед турбиной до 1300 К при неизменных прочих исходных данных работа идеального цикла будет равна 365,9 кДж/кг при оптимальном значении πк=13,98. То есть, при повышении T3 работа цикла увеличивается, но также повышается и оптимальное πк.
На рис. 4 представлены результаты расчёта реального цикла ГТУ при тех же исходных данных (которые введены в поля программы на рис. 2).
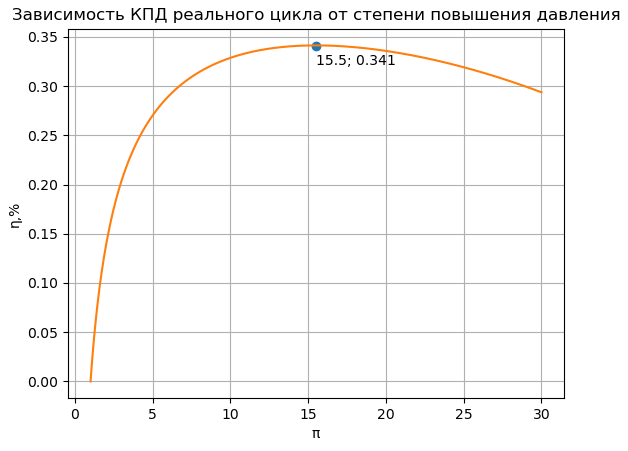
Рис. 4. Зависимость КПД реального цикла Брайтона от степени повышения давления в компрессоре.
В данном случае главным оптимизируемым параметром реального цикла является внутренний КПД установки. Видим, что он равен 34,1% при степени повышения давления в компрессоре 15,5.
Для сравнения – при повышении температуры перед турбиной до 1300 К достижимый коэффициент полезного действия ГТУ равен 36,6% при πк=19,08. Как и в случае идеального цикла, повышение Т3 приводит к повышению КПД, но при увеличении оптимальной степени повышения давления.
Также видно, что при постоянной температуре перед турбиной небольшое снижение или повышение давления воздуха перед камерой сгорания не приводит к сильному изменению КПД, который существенно снижается лишь при очень низких значениях степени повышения давления в компрессоре.
Описанные и проверенные на примере явления качественного влияния характеристик цикла на КПД приводятся в литературных источниках, например, в книге [9].
В случае необходимости, с использованием вышеописанного подхода к реализации методик расчёта газотурбинных установок на языке Python с подключением описанных и дополнительных библиотек, можно рассчитать и вывести в графическом виде и другие характеристики цикла Брайтона.
Обсуждение. Таким образом, проведённая работа доказывает удобство использования языка Python для создания программы расчёта термодинамического цикла. Результаты расчёта примера полностью соответствуют данным, описанным в книге [3].
Созданная программа позволяет оптимизировать характеристики как идеального (с изоэнтропными процессами подвода и отвода теплоты), так и реального (с подводом и отводом теплоты в адиабатных процессах) цикла Брайтона при любых сочетаниях заданных исходных параметров с целью достижения его наибольшего термодинамического совершенства.
Полученный результат оптимизации является предварительным и позволяет произвести в дальнейшем детальные проектные расчёты элементов газотурбинной установки с выбранными характеристиками.
Заключение. В процессе выполнения работы с использованием описанных в литературе «классических» методик расчёта идеального и реального циклов Брайтона разработана программа на языке Python с использованием дополнительных библиотек, позволяющая решать следующие задачи:
- определять состав исходных данных, необходимых для расчёта циклов газотурбинных установок;
- визуализировать характеристики разрабатываемого цикла Брайтона;
- подобрать оптимальные характеристики исследуемого цикла;
- наглядно продемонстрировать влияние варьируемых исходных факторов на показатели эффективности цикла.
Программа позволяет строить как характеристики уже используемых установок, так и проектировать новые газотурбинные двигатели и установки, работающие по циклу Брайтона. Достигнутая автоматизация при её внедрении приводит к уменьшению трудозатрат на этапе проектирования газотурбинных установок, а также к повышению их надёжности и эффективности работы [10]. Разработанная программа может использоваться при изучении основ термодинамики студентами вузов, персоналом, проектирующим и обслуживающим ГТУ и как наглядная иллюстрация применения языка Python для проведения теплофизических расчётов.
Библиографическая ссылка
Ильичев В.Ю., Юрик Е.А. ИССЛЕДОВАНИЕ И ОПТИМИЗАЦИЯ ТЕРМОДИНАМИЧЕСКОГО ЦИКЛА ГАЗОТУРБИННОГО ДВИГАТЕЛЯ // Научное обозрение. Физико-математические науки . 2020. № 1. С. 2-2;URL: https://physics-mathematics.ru/ru/article/view?id=90 (дата обращения: 05.01.2026).
 science-review.ru
science-review.ru